Ultrashort Pulses

Ultrashort pulses are usually generated with passively mode-locked lasers, but sometimes also with optical parametric amplifiers (possibly using a supercontinuum as input) or with free electron lasers. It is also possible to start with longer pulses and apply some method of pulse compression. The article on ultrafast lasers lists some important areas of ultrashort pulse generation, including the generation of few-cycle pulses, where the pulse duration is only a small multiple of an optical cycle (few-cycle pulses).

Intrinsically, ultrashort pulses have a broad optical bandwidth. Even if they are instantaneous frequency is nearly constant throughout the pulse duration, the optical spectrum has a width which is at least of the order of the inverse pulse duration. This is essentially because e.g. for resonantly exciting some medium, a change of optical frequency matters only if it is large enough to cause a significant phase change within the pulse duration [1].

In many cases, the instantaneous frequency of a pulse is approximately constant, and the time–bandwidth product is somewhat below unity. For example, an unchirped Gaussian pulse with a 1 ps pulse duration (full width at half maximum) has an optical bandwidth of ≈0.44 THz. Extremely short pulses (few-cycle pulses) can have octave-spanning optical spectra.

Concerning their spatial properties, ultrashort pulses are usually generated in the form of laser beams. Essentially, they can be focused to very small spots just as it is possible with stationary beams. However, various limitations come into play particularly in the regime of few-cycle pulses. For example, the broad optical bandwidth of such pulses leads to problems with the chromatic dispersion of lens materials, which leads to chromatic aberrations of the focusing optics unless special correction techniques are employed. This can lead to complicated spatio-temporal effects, which may make the focused pulse to have a larger duration than the pulse before focusing. Possible measures against such distortions include the use of reflective or diffractive (instead of refractive) optics as well as the careful compensation of various types of aberrations, e.g. using suitable lens combinations.

The propagation of ultrashort pulses in media gives rise to a range of interesting phenomena, particularly when optical nonlinearities are involved. This can be investigated with, e.g., pulse propagation modeling. Relevant physical effects can be chromatic dispersion, the Kerr effect, Raman scattering, and gain saturation, to name just some important examples.

When ultrashort pulses are generated in a mode-locked laser, instead laser they can be subject to various pulse shaping phenomena. For example, there is often a saturable absorber which causes high losses to the beginning and sometimes also the end of the pulse.

Outside the laser, ultrashort pulses can further be manipulated with various kinds of pulse shapers.

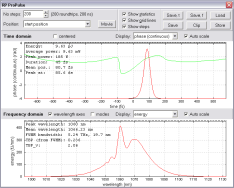
There are various methods for pulse characterization. While some only allow the measurement of fundamental pulse parameters such as the pulse duration, others can be used for “complete” characterization in the sense that the whole time-dependent electric field and the spectral phase can be obtained. The results can be visualized in various ways, e.g. with graphs of time- or frequency-dependent functions, or with spectrograms.

Most frequently, one measures pulse durations using autocorrelators.

By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.

(Suggest additional literature!)