Mode Locking

Active mode locking involves the periodic modulation of the resonator losses or of the round-trip phase change, achieved e.g. with an acousto-optic or electro-optic modulator, a Mach–Zehnder integrated-optic modulator, or a semiconductor electroabsorption modulator. If the modulation is synchronized with the resonator round trips, this can lead to the generation of ultrashort pulses, usually with picosecond pulse durations. In most but not all cases, the pulse duration achieved is governed by a balance of pulse shortening through the modulator and pulse broadening via other effects, such as the limited gain bandwidth.

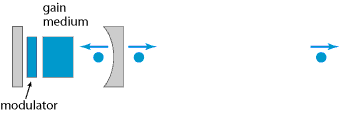
Passive mode locking (with a saturable absorber) allows the generation of much shorter (femtosecond) pulses, basically because a saturable absorber, driven by already short pulses, can modulate the resonator losses much faster than an electronic modulator: the shorter the pulse becomes, the faster the loss modulation, provided that the absorber has a sufficiently short recovery time. The pulse duration can be even well below the recovery time of the absorber. In some cases, reliable self-starting mode locking is not achieved.

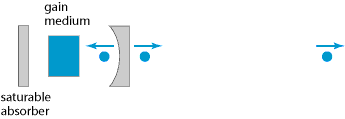
More details can be found in the articles on active mode locking and passive mode locking.

In some lasers (particularly in mode-locked diode lasers), active and passive mode locking are simultaneously applied. Such hybrid mode-locked lasers combine some key advantages, such as an externally controlled pulse repetition rate and fairly short pulses.

Most mode-locked lasers are continuously pumped, often with a laser diode. The pump source then continuously supplies energy to the gain medium, while the circulating pulse extracts energy in regular time intervals. In most cases, the pulse spacing is very short compared with the upper-state lifetime, so that the gain medium can easily store the energy during such times. Gain saturation will then be the same as for continuous laser emission with the same average power.

Even some gain media with a fairly short upper-state lifetime, e.g. in dye lasers or some semiconductor lasers (e.g. VECSELs), continuous pumping is possible, provided that the pulse repetition rate is not too low. If this condition can not be fulfilled, so that gain saturation by a single pulse becomes strong (which can make the pulse formation unstable), synchronous pumping can be a solution. This, however, requires another mode-locked laser as the pump source.

High repetition rate pulse trains are sometimes obtained with harmonic mode locking, where multiple pulses are circulating in the laser resonator with a constant temporal spacing. This allows the generation of multi-gigahertz pulse trains even with fiber lasers, which typically have fundamental round-trip frequencies of only some tens of megahertz.

For high pulse repetition rates with fundamental mode locking, i.e., without harmonic mode locking, very short laser resonators are required. If Q-switching instabilities are avoided with a proper design, such lasers can be very simple, stable and compact.

Due to the high pulse repetition rate, the pulse energies obtained from mode-locked lasers are fairly limited – normally nanojoules or picojoules. Higher pulse energies combined with lower repetition rates can be obtained with cavity-dumped mode-locked lasers and with regenerative amplifiers.

The optical spectrum of a pulse train, as generated in a mode-locked laser, is not smooth (as for a single pulse), but rather consists of discrete lines with an exactly constant spacing which equals the pulse repetition rate (→ frequency combs). This is true although the resonance frequencies of the resonator modes are usually not exactly equidistant due to the effect of chromatic dispersion, e.g. in the gain medium: the mode-locking mechanism forces the laser to emit frequencies which can to some extent deviate from the frequencies of the resonator modes. These frequency deviations may not be arbitrarily high, and therefore the generation of broadband spectra is usually possible only if the resonator dispersion is sufficiently small, so that the resonator mode frequencies are approximately equidistant. In the time domain, this condition can be understood via the temporal broadening of pulses caused by dispersion, which must be compensated by the mode-locking mechanism. Note, however, that optical nonlinearities often also play an important role, so that considering the “cold cavity modes” misses an important part of the physical mechanisms.

The term mode locking originates from a description in the frequency domain: a short pulse is formed in the laser resonator when a fixed phase relationship is achieved between its longitudinal modes, or more precisely, between the lines in the spectrum of the laser output. However, the basic mechanisms leading to mode locking can usually be much more easily understood in the time domain. Also, the concept of resonator modes becomes questionable under the influence of strong optical nonlinearities. Strictly, it is not even advisable to use the term modes for the lines in the spectrum of a mode-locked laser, even though these lines are related to the resonator modes.

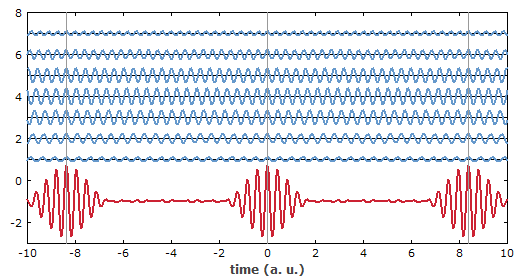
It is instructive to consider the synthesis of a periodic pulse train by superposition of sinusoidal oscillations (Figure 4) with equally spaced frequencies, corresponding to different axial resonator modes in a mode-locked laser. The larger the number of frequency components involved, the shorter can be the duration of the generated pulses.

An important aspect is that there must be a fixed phase relationship between these modes. This is illustrated in Figure 5: the blue curve shows a pulse train with a fixed phase relationship, so that at regular temporal positions (e.g. at t = 0) the electric fields of all frequency components add up to a maximum of the total field strength. The red curve shows the electric field for the same strength of all frequency components, but with random relative phases.

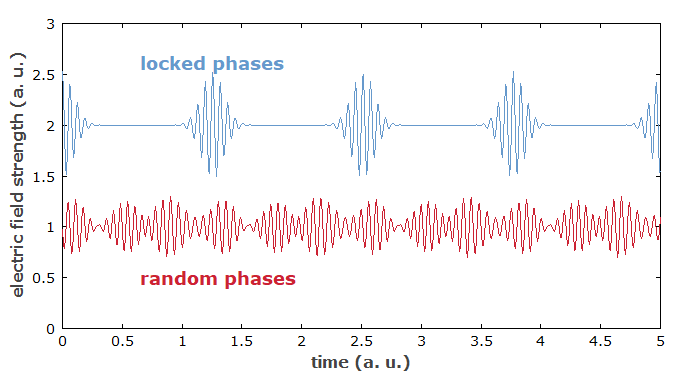
Due to chromatic dispersion, the axial modes of a laser resonator would normally not have exactly equidistant mode frequencies, and therefore the mentioned phase relationship should normally be lost within a short time. However, that phase relationship can be enforced by a strong enough mode-locking mechanism provided that the dephasing tendencies are not too strong. The frequencies of the lines in the optical spectrum are then exactly equidistant (disregarding noise), thus slightly deviating from the mode frequencies.

The various mechanisms for mode locking can exhibit various kinds of instabilities. For example, a laser may generate bunches of pulses (instead of single pulses), pulses with unstable energy (→ Q-switching instabilities), pulses which fall apart after some time and are later replaced with new pulses, or pulses which are accompanied by a noise background. Different kinds of modeling can be very helpful in tracking down such problems and to find appropriate remedies.

Even without particular instabilities, the output of a mode-locked laser contains various kinds of noise; the timing jitter (random fluctuations of the pulse positions) is often of special interest. Other types of noise include phase noise, intensity noise, and fluctuations of other parameters such as the pulse duration, chirp, and optical center frequency. The phase noise results in a finite width of the lines in the generated frequency comb. There are interesting relations between different types of noise in mode-locked lasers [16].

Note that the article on mode-locked lasers contains some more details on different kinds of mode-locked lasers, and more details concerning mode-locking techniques can be found in the articles on active and passive mode locking.

Optimum mode-locked performance depends on a well worked-out laser design, including the choice of a suitable mode locking device, be it some kind of modulator or a saturable absorber. The article on mode locking devices gives more details.

Your question or comment:

Spam check:

  (Please enter the sum of thirteen and three in the form of digits!)

By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.

[1]	W. E. Lamb Jr., “Theory of an optical laser”, Phys. Rev. 134 (6A), A1429 (1964), doi:10.1103/PhysRev.134.A1429 (proposed the technique of mode locking)
[2]	L. E. Hargrove, R. L. Fork, and M. A. Pollack, “Locking of He–Ne laser modes induced by synchronous intracavity modulation”, Appl. Phys. Lett. 5, 4 (1964), doi:10.1063/1.1754025 (first report of active mode locking)
[3]	M. DiDomenico, “Small-signal analysis of internal (coupling type) modulation of lasers”, J. Appl. Phys. 35 (10), 2870 (1964), doi:10.1063/1.1713121
[4]	D. J. Kuizenga and A. E. Siegman, “FM and AM mode locking of the homogeneous laser – Part I: theory”, IEEE J. Quantum Electron. 6 (11), 694 (1970), doi:10.1109/JQE.1970.1076343
[5]	E. P. Ippen, C. V. Shank, and A. Dienes, “Passive mode locking of the cw dye laser”, Appl. Phys. Lett. 21, 348 (1972), doi:10.1063/1.1654406 (first continuous-wave mode locking with a saturable absorber)
[6]	B. K. Garside and T. K. Lim, “Laser mode locking using saturable absorbers”, JAP 44 (5), 2335 (1973), doi:10.1063/1.1662561
[7]	G. H. C. New, “Pulse evolution in mode-locked quasi-continuous lasers”, IEEE J. Quantum Electron. 10 (2), 115 (1974), doi:10.1109/JQE.1974.1145781
[8]	L. F. Mollenauer and R. H. Stolen, “Soliton laser”, Opt. Lett. 9 (1), 13 (1984), doi:10.1364/OL.9.000013
[9]	J. G. Fujimoto, A. M. Weiner, and E. P. Ippen, “Generation and measurement of optical pulses as short as 16 fs”, Appl. Phys. Lett. 44, 832 (1984), doi:10.1063/1.94957
[10]	R. L. Fork et al., “Compression of optical pulses to six femtoseconds by using cubic phase compensation”, Opt. Lett. 12 (7), 483 (1987), doi:10.1364/OL.12.000483
[11]	H. A. Haus, “Mode-locking of lasers”, J. Sel. Top. Quantum Electron. 6 (6), 1173 (2000), doi:10.1109/2944.902165
[12]	R. Paschotta, “Passive mode locking with slow saturable absorbers”, Appl. Phys. B 73 (7), 653 (2001), doi:10.1007/s003400100726
[13]	R. Paschotta et al., “Soliton-like pulse shaping mechanism in passively mode-locked surface-emitting semiconductor lasers”, Appl. Phys. B 75, 445 (2002), doi:10.1007/s00340-002-1014-5
[14]	R. Paschotta, “Noise of mode-locked lasers. Part I: numerical model”, Appl. Phys. B 79, 153 (2004); R. Paschotta, “Noise of mode-locked lasers. Part II: timing jitter and other fluctuations”, Appl. Phys. B 79, 163 (2004), doi:10.1007/s00340-004-1548-9
[15]	N. Usechak and G. Agrawal, “Semi-analytic technique for analyzing mode-locked lasers”, Opt. Express 13 (6), 2075 (2005), doi:10.1364/OPEX.13.002075
[16]	R. Paschotta et al., “Optical phase noise and carrier–envelope offset noise of mode-locked lasers”, Appl. Phys. B 82 (2), 265 (2006), doi:10.1007/s00340-005-2041-9
[17]	R. Paschotta and U. Keller, “Passively mode-locked solid-state lasers”, in Solid-State Lasers and Applications (ed. A. Sennaroglu), CRC Press, Boca Raton, FL (2007), Chapter 7, pp. 259–318
[18]	R. Paschotta, Field Guide to Laser Pulse Generation, SPIE Press, Bellingham, WA (2007)
[19]	R. Paschotta, case study on active mode locking
[20]	R. Paschotta, case study on passive mode locking

(Suggest additional literature!)

This encyclopedia is authored by Dr. Rüdiger Paschotta, the founder and executive of RP Photonics Consulting GmbH. How about a tailored training course from this distinguished expert at your location? Contact RP Photonics to find out how his technical consulting services (e.g. product designs, problem solving, independent evaluations, training) and software could become very valuable for your business!