Frequency Combs
Definition: optical spectra consisting of equidistant lines
German: Frequenzkämme
Categories: light pulses, methods
How to cite the article; suggest additional literature
Author: Dr. Rüdiger Paschotta
Frequency combs have become a hot topic in research, and have attracted even more attention since the Nobel Prize in Physics was awarded to Roy J. Glauber, John L. Hall and Theodor W. Hänsch in 2005. The latter two have made pioneering contributions to the development of the optical frequency comb technique.
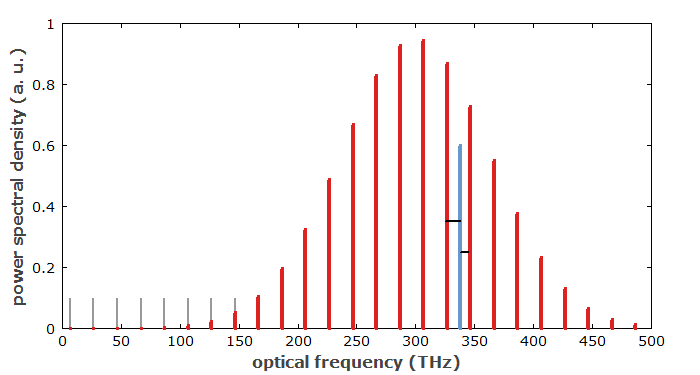
An optical frequency comb is an optical spectrum which consists of equidistant lines (Figure 1), i.e., it has equidistant optical frequency components, while the intensity of the comb lines can vary substantially. Usually, such kind of optical spectrum is associated with a regular train of ultrashort pulses, having a fixed pulse repetition rate which determines the inverse line spacing in the spectrum. To understand how such a spectral shape arises, one has to consider the properties of Fourier transforms, translating the complex amplitudes from the time domain to the frequency domain (see also the Spotlight article of 2007-10-11).
A frequency comb can be used as an optical ruler: If the comb frequencies are known, the frequency comb can be used e.g. to measure unknown frequencies by measuring beat notes, which reveal the difference in frequency between the unknown frequency and the comb frequencies. For performing such measurements in a wide frequency range, a large overall bandwidth of the frequency comb is needed.
Early attempts to produce broadband frequency combs were based on strongly driven electro-optic modulators, which can impose dozens of sidebands on a single-frequency input beam from a single-frequency continuous-wave laser. It was then found that this process could be made more efficient (for obtaining more comb lines) by placing the modulator in a resonant cavity, particularly when the intracavity dispersion was minimized. Further improvements were based on parametric amplification.
Such devices acquired an increasing similarity to mode-locked lasers for ultrashort pulse generation, and in fact it was then realized that a femtosecond mode-locked laser can actually be used very well for generating very broadband frequency combs: the optical spectrum of a periodic pulse train, as generated in a mode-locked laser, consists of discrete lines with an exactly constant spacing which equals the pulse repetition frequency. If the pulse duration gets far below 1 ps, the optical spectrum becomes very wide, leading to a very broad frequency comb. Using strong nonlinearities outside the laser resonator, one can further broaden the comb. Frequently, one uses supercontinuum generation in optical fibers (often photonic crystal fibers) for such spectral broadening, and this often leads to octave-spanning optical spectra.
Note that the generation of a frequency comb requires that the periodicity applies not only to the pulse envelopes, but to the whole electric field of the pulses, including their optical phase, apart from a constant phase slip as to be discussed in the following. In other words, coherence between the pulses is required. Typically, pulses from mode-locked lasers exhibit a very high degree of mutual coherence, with random phase changes evolving only during many resonator round-trips. The effects of residual noise on the comb is discussed further below.
The Carrier–Envelope Offset
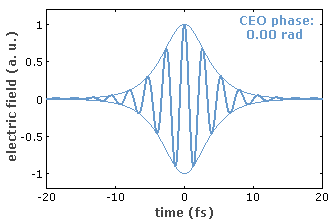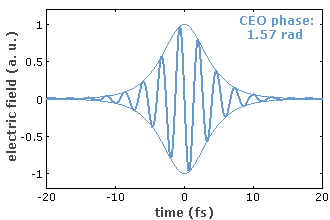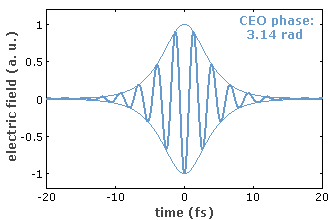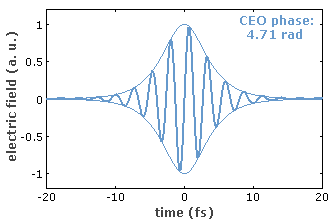
If the pulse train were perfectly periodic – not only concerning the intensity versus time but also with respect to the electric field –, all the frequencies of the lines in the spectrum would be integer multiples (harmonics) of the pulse repetition rate. In most cases, however, intracavity dispersion and nonlinearities cause a slip of the carrier–envelope offset (CEO) from pulse to pulse, i.e., the oscillations of the electric field are constantly shifted with respect to the pulse envelope (Figure 2). If the change in the carrier–envelope offset per resonator round trip is a constant (denoted Δφceo), all optical line frequencies can be written as
where j is an integer index, frep is the pulse repetition rate and
is the CEO frequency, which according to this definition can be between 0 and frep.
If the two parameters frep and νceo are known, all frequencies of the comb are also known. In that case, any optical frequency within the range of the frequency comb can be determined by recording a beat note between the unknown frequency and the comb. The lowest beat frequency is the distance from the unknown frequency to the nearest line of the comb (see Figure 1). An approximate frequency measurement (e.g. with a wavemeter) can be used to determine from which line the detected beat note originates. It is then possible to find out whether the unknown frequency is above or below the comb line frequency, e.g. by observing the changes in beat frequency when tuning the unknown frequency or the comb position.
The pulse repetition rate frep is easily measured with a fast photodiode, whereas the measurement of νceo is significantly more difficult. It can be detected e.g. via an interferometric f−2f self-referencing scheme [4, 5], where one uses a beat note between the frequency-doubled lower-frequency end of the comb spectrum with the higher-frequency end (Figure 3), if the spectrum covers an optical octave. (Modified methods, using e.g. a 2f−3f self-referencing scheme, involve a beat note between different harmonics of the laser light.) Such broad spectra can be achieved e.g. with supercontinuum generation in photonic crystal fibers, if the laser output itself does not have sufficient bandwidth. It is possible, however, to generate octave-spanning spectra directly with titanium–sapphire lasers [10].
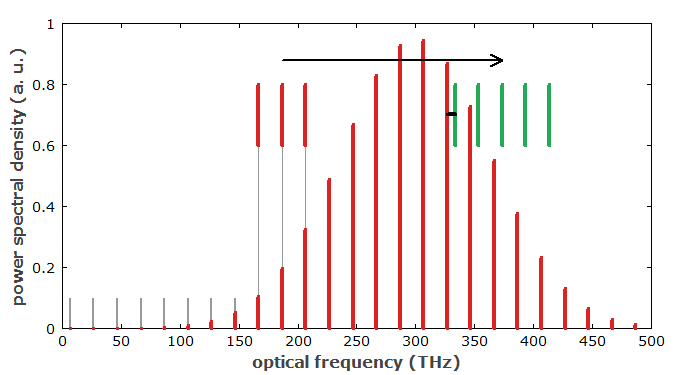
Note that not all applications of frequency combs require the measurement of the CEO frequency. For example, some applications in laser spectroscopy [1, 40, 55] are not dependent on that.
CEO Stabilization
For some applications, the CEO frequency is stabilized with a feedback system, using an error signal e.g. from an f−2f interferometer. The CEO frequency may be fixed at zero or at any given value, or at a certain fraction of the pulse repetition rate. The weaker form of CEO stabilization means that the excursions of the CEO frequency are limited, but the CEO phase may still drift away. The stronger form is real CEO phase stabilization [8, 9, 12], where the CEO phase either stays fixed or advances from pulse to pulse by a predictable value. Here, the uncertainty in the CEO phase should be well below 1 rad. Note that even with a stabilization based on feedback from the error signal obtained with an f−2f interferometer (see above) may be unable to prevent drifts of the CEO phase, e.g. due to thermal drifts in the nonlinear crystal used.
A totally different way of obtaining a CEO-stabilized frequency comb is to do difference frequency generation of different parts of the comb spectrum. In that case, the nonlinear mixing product has a zero CEO frequency.
When CEO-stabilized pulses are sent through a high-gain amplifier, e.g. a regenerative amplifier in a CPA setup, the CEO phase stability may be lost in the amplifier. However, it is possible to construct amplifiers which well preserve the CEO phase [28].
Note that even a free-running (i.e. not CEO-stabilized) frequency comb can be used for ultraprecise measurements, e.g. in an optical clockwork. Here, one only monitors deviations of CEO phase and repetition rate and corrects the resulting errors e.g. on a beat signal [15, 23]. This correction may be performed either with purely electronic means or on a computer. The principle of a free-running transfer oscillator has two basic advantages: it does not require CEO stabilization, and it works up to very high noise frequencies beyond the bandwidth of a feedback system.
Noise in Frequency Combs
The issue of noise in the lines of a frequency comb is complex and interesting. Different noise sources, such as mirror vibrations, thermal drifts, pump intensity noise and quantum noise, cause different and partly correlated combinations of noise of the pulse repetition rate and the carrier–envelope offset frequency. In addition, there is some level of noise in all lines of a frequency comb which is not correlated.
For example, resonator length changes have hardly any impact on the CEO frequency but influence the pulse repetition rate, i.e. the line spacing. This means that the lines move in the Fourier spectrum as if they were fixed on a rubber band [15], the left end of which is fixed near ν = 0 while someone is pulling the other end. There is a so-called fixed point near ν = 0. For thermal drifts, the position of the fixed point may be totally different; in a fiber laser, for example, it can be located well above the optical frequencies of the comb. Phase changes which are related to intensity changes via the Kerr effect are associated with yet another fixed point.
To some extent, the rubber band model can be applied also to noise in a more general context. In particular, quantum noise (originating e.g. from spontaneous emission in the gain medium) acting in a laser with relatively long pulses (not few-cycle pulses) causes phase changes of the lines which can be approximately described by a fixed point near the optical center frequency of the spectrum, although there is some additional noise not described by this fixed point. Phase changes corresponding to the mentioned fixed point correspond to timing jitter, but not of the same kind as can be caused by cavity length fluctuations, because the fixed points are at very different locations in the spectrum. A consequence of this is that the compensation of quantum-induced timing jitter by cavity length control will cause very strong noise of the CEO frequency [26].
Another important theoretical finding is that the quantum-limited CEO noise of mode-locked lasers with relatively long pulses is larger than from a laser with few-cycle pulses but otherwise similar parameters. Indeed, there is substantial experimental evidence for significantly stronger noise from fiber lasers as compared with titanium–sapphire lasers, which generate shorter pulses. However, there is also a significant impact of pump noise on fiber lasers. In addition, further spectral broadening of a fiber laser output in a photonic crystal fiber can introduce extra noise.
Concerning the description of noise in a frequency comb, there are some caveats related to the notion of CEO noise. The clearest and most rigorous approach considers the noise in all lines of the spectrum as the fundamental phenomenon. Timing jitter and CEO noise can then be seen as projections of this noise to different one-dimensional sub-spaces [26].
Note that there is an article concerning noise in ultrashort pulses in the Photonics Spotlight.
Applications of Frequency Combs in Metrology and Other Areas
As shown above, frequency combs can be used for the measurement of absolute optical frequencies. More precisely, this means that optical frequencies are related to the microwave frequency e.g. from a cesium clock. In other words, a frequency comb can serve as an optical clockwork. Frequency combs can also be used to measure ratios of optical frequencies with extremely high precision, which is not even limited by laser noise [13]. Apart from frequency metrology, other applications are possible in high-precision spectroscopy [36, 40], optical sensing, distance measurements [29], laser noise characterization, telecommunications, and in fundamental physics.
Desirable properties of a frequency comb source for such applications are:
- It should cover the optical frequency range of interest.
- One should be able to accurately measure the CEO frequency (typically with an f−2f interferometer, requiring a large spectral width of the laser).
- The required comb lines should have sufficiently high optical powers.
- The influences of noise (both quantum noise and technical noise sources) should be as weak as possible.
- It is often required that the comb parameters can be rapidly adjusted e.g. within a feedback loop.
The first self-referenced frequency combs for metrology were generated with Ti:sapphire lasers. In most cases, their output spectra are very broad but not yet octave-spanning, as required for detecting the CEO frequency with the usual f–2f self-referencing scheme. Additional spectral broadening in a photonic crystal fiber is then used. Initially, there was a concern that this method would not preserve the coherence and thus the comb structure, but it was found that the comb structure is usually well preserved, even though noise added in the spectral broadening processes is still a subject of investigation.
More recently, erbium-doped fiber lasers have also been used in conjunction with a photonic crystal fiber or a highly nonlinear dispersion-flattened fiber for spectral broadening. Fiber sources have the potential for a more practical, robust and compact setup, as required for real-world applications. However, titanium–sapphire-based systems usually exhibit better noise performance (see above). The influence of quantum noise on the carrier–envelope offset is fundamentally stronger for pulses with longer durations, which most fiber lasers generate.
In 2005, the extension of frequency combs into the vacuum ultraviolet region was demonstrated by high harmonic generation in a femtosecond enhancement cavity [24].
For generating frequency combs with very large frequency spacings of many gigahertz, one can use micro-resonators, having a correspondingly short round-trip time. Such a device can be pumped with a single-frequency beam, and a substantial number of comb lines can be generated based on the Kerr nonlinearity [14]; such frequency combs are sometimes called Kerr combs. The obtained comb lines are usually not mutually coherent. However, it is possible to obtain a high degree of coherence through mode-locked operation in certain regimes [47], where one effectively has a mode-locked laser based on parametric amplification, or in other words an optical parametric oscillator, where dissipative Kerr solitons are generated in a resonator with anomalous chromatic dispersion. This mode-locking regime requires careful tuning of the pump laser. Due to the very high Q factors, such devices can have very low noise. They can, for example, be applied as comb sources for optical fiber communications with wavelength division multiplexing; for example, a system transmitting more than 50 Tbit/s distributed over 179 optical carriers with 100 GHz spacing (produced with two similar resonators) has been demonstrated [54].
Frequency comb laser sources are commercially available from different sources and are beginning to be widely used for metrology purposes. As high-precision time measurements are becoming technologically more and more important – consider the GPS system and the European Galileo project as examples – and other new applications also appear to be very advantageous, it is to be expected that frequency combs will maintain high technological importance.
Suppliers
The RP Photonics Buyer's Guide contains 15 suppliers for frequency comb sources. Among them:
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here; we would otherwise delete it soon. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
Bibliography
| [1] | J. N. Eckstein, A. I. Ferguson, and T. W. Hänsch, “High-resolution two-photon spectroscopy with picosecond light pulses”, Phys. Rev. Lett. 40 (13), 847 (1978), doi:10.1103/PhysRevLett.40.847 |
| [2] | T. Udem et al., “Absolute optical frequency measurement of the cesium D-1 line with a mode-locked laser”, Phys. Rev. Lett. 82 (18), 3568 (1999), doi:10.1103/PhysRevLett.82.3568 |
| [3] | H. R. Telle et al., “Carrier–envelope offset phase control: a novel concept for absolute optical frequency measurement and ultrashort pulse generation”, Appl. Phys. B 69, 327 (1999), doi:10.1007/s003400050813 |
| [4] | D. J. Jones et al., “Carrier–envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis”, Science 288, 635 (2000), doi:10.1126/science.288.5466.635 |
| [5] | R. Holzwarth et al., “Optical frequency synthesizer for precision spectroscopy”, Phys. Rev. Lett. 85 (11), 2264 (2000), doi:10.1103/PhysRevLett.85.2264 |
| [6] | S. A. Diddams et al., “Direct link between microwave and optical frequencies with a 300 THz femtosecond laser comb”, Phys. Rev. Lett. 84 (22), 5102 (2000), doi:10.1103/PhysRevLett.84.5102 |
| [7] | L. Hollberg et al., “Optical frequency standards and measurements”, IEEE J. Quantum Electron. 37 (12), 1502 (2001), doi:10.1109/3.970895 |
| [8] | A. Poppe et al., “Few-cycle optical waveform synthesis”, Appl. Phys. B 72, 373 (2001), doi:10.1007/s003400000526 |
| [9] | U. Morgner et al., “Nonlinear optics with phase-controlled pulses in the sub-two-cycle regime”, Phys. Rev. Lett. 86 (24), 5462 (2001), doi:10.1103/PhysRevLett.86.5462 |
| [10] | R. Ell et al., “Generation of 5-fs pulses and octave-spanning spectra directly from a Ti:sapphire laser”, Opt. Lett. 26 (6), 373 (2001), doi:10.1364/OL.26.000373 |
| [11] | R. Holzwarth et al., “Optical clockworks and the measurement of laser frequencies with a mode-locked frequency comb”, IEEE J. Quantum Electron. 37 (12), 1493 (2001), doi:10.1109/3.970894 |
| [12] | F. W. Helbing et al., “Carrier–envelope offset dynamics and stabilization of femtosecond pulses”, Appl. Phys. B 74, S35 (2002), doi:10.1007/s00340-002-0898-4 |
| [13] | J. Stenger et al., “Ultraprecise measurement of optical frequency ratios”, Phys. Rev. Lett. 88 (7), 073601 (2002), doi:10.1103/PhysRevLett.88.073601 |
| [14] | P. Del’Haye et al., “Optical frequency comb generation from a monolithic microresonator”, Nature 450, 1214 (2007), doi:10.1038/nature06401 |
| [15] | H. R. Telle et al., “Kerr-lens mode-locked lasers as transfer oscillators for optical frequency measurements”, Appl. Phys. B 74, 1 (2002), doi:10.1007/s003400100735 |
| [16] | T. M. Ramond et al., “Phase-coherent link from optical to microwave frequencies by means of the broadband continuum from a 1-GHz Ti:sapphire femtosecond oscillator”, Opt. Lett. 27 (20), 1842 (2002), doi:10.1364/OL.27.001842 |
| [17] | T. M. Fortier et al., “Phase stabilization of an octave-spanning Ti:sapphire laser”, Opt. Lett. 28 (22), 2198 (2003), doi:10.1364/OL.28.002198 |
| [18] | F. W. Helbing et al., “Carrier–envelope offset phase-locking with attosecond timing jitter”, J. Sel. Top. Quantum Electron. 9 (4), 1030 (2003), doi:10.1109/JSTQE.2003.819104 |
| [19] | S. T. Cundiff and Jun Ye, “Colloquium: femtosecond optical frequency combs”, Rev. Mod. Phys. 75, 325 (2003), doi:10.1103/RevModPhys.75.325 |
| [20] | J. Ye et al., “Optical frequency combs: from frequency metrology to optical phase control”, J. Sel. Top. Quantum Electron. 9 (4), 1041 (2003), doi:10.1109/JSTQE.2003.819109 |
| [21] | L. Matos et al., “Direct frequency comb generation from an octave-spanning, prismless Ti:sapphire laser”, Opt. Lett. 29 (14), 1683 (2004), doi:10.1364/OL.29.001683 |
| [22] | T. R. Schibli et al., “Frequency metrology with a turnkey all-fiber system”, Opt. Lett. 29 (21), 2467 (2004), doi:10.1364/OL.29.002467 |
| [23] | E. Benkler et al., “Circumvention of noise contributions in fiber laser based frequency combs”, Opt. Express 13 (15), 5662 (2005), doi:10.1364/OPEX.13.005662 |
| [24] | R. J. Jones et al., “Phase-coherent frequency combs in the vacuum ultraviolet via high-harmonic generation inside a femtosecond enhancement cavity”, Phys. Rev. Lett. 94 (19), 193201 (2005), doi:10.1103/PhysRevLett.94.193201 |
| [25] | O. D. Mücke et al., “Self-referenced 200 MHz octave-spanning Ti:sapphire laser with 50 attosecond carrier–envelope phase jitter”, Opt. Express 13 (13), 5163 (2005), doi:10.1364/OPEX.13.005163 |
| [26] | R. Paschotta et al., “Optical phase noise and carrier–envelope offset noise of mode-locked lasers”, Appl. Phys. B 82 (2), 265 (2006) (explaining e.g. why longer pulses are associated with higher CEO noise), doi:10.1007/s00340-005-2041-9 |
| [27] | T. M. Fortier et al., “Octave-spanning Ti:sapphire laser with a repetition rate > 1 GHz for optical frequency measurements and comparisons”, Opt. Lett. 31 (7), 1011 (2006), doi:10.1364/OL.31.001011 |
| [28] | E. Gagnon et al., “Long-term carrier–envelope phase stability from a grating-based, chirped pulse amplifier”, Opt. Lett. 31 (12), 1866 (2006), doi:10.1364/OL.31.001866 |
| [29] | T. R. Schibli et al., “Displacement metrology with sub-pm resolution in air based on a fs-comb wavelength synthesizer”, Opt. Express 14 (13), 5984 (2006), doi:10.1364/OE.14.005984 |
| [30] | R. Paschotta, “Frequenzkämme und optische Frequenzmetrologie”, Photonik 3 / 2006, p. 60 |
| [31] | J. J. McFerran et al., “Elimination of pump-induced frequency jitter on fiber-laser frequency combs”, Opt. Lett. 31 (13), 1997 (2006), doi:10.1364/OL.31.001997 |
| [32] | W. C. Swann et al., “Fiber-laser frequency combs with subhertz relative linewidths”, Opt. Lett. 31 (20), 3046 (2006), doi:10.1364/OL.31.003046 |
| [33] | D. R. Walker et al., “Frequency dependence of the fixed point in a fluctuating frequency comb”, Appl. Phys. B 89, 535 (2007), doi:10.1007/s00340-007-2882-5 |
| [34] | N. R. Newbury and W. C. Swann, “Low-noise fiber-laser frequency combs”, J. Opt. Soc. Am. B 24 (8), 1756 (2007), doi:10.1364/JOSAB.24.001756 |
| [35] | S. Ozharar et al., “Ultraflat optical comb generation by phase-only modulation of continuous-wave light”, IEEE J. Lightwave Technol. 20 (1), 36 (2008), doi:10.1109/LPT.2007.910755 |
| [36] | I. Coddington et al., “Coherent multiheterodyne spectroscopy using stabilized optical frequency combs”, Phys. Rev. Lett. 100 (1), 013902 (2008), doi:10.1103/PhysRevLett.100.013902 |
| [37] | M. J. Thorpe and J. Ye, “Cavity-enhanced direct frequency comb spectroscopy”, Appl. Phys. B 91, 397 (2008), doi:10.1007/s00340-008-3019-1 |
| [38] | T. R. Schibli et al., “Optical frequency comb with submillihertz linewidth and more than 10 W average power”, Nature Photon. 2, 355 (2008), doi:10.1038/nphoton.2008.79 |
| [39] | L. Chen et al., “Octave-spanning, dual-output 2.166 GHz Ti:sapphire laser”, Opt. Express 16 (25), 20699 (2008), doi:10.1364/OE.16.020699 |
| [40] | J. Mandon et al., “Fourier transform spectroscopy with a frequency comb”, Nature Photon. 3, 99 (2009), doi:10.1038/nphoton.2008.293 |
| [41] | A. Ruehl et al., “80 W, 120 fs Yb-fiber frequency comb”, Opt. Lett. 35 (18), 3015 (2010), doi:10.1364/OL.35.003015 |
| [42] | S. A. Diddams, “The evolving optical frequency comb”, J. Opt. Soc. Am. B 27 (11), B51 (2010), doi:10.1364/JOSAB.27.000B51 |
| [43] | K. Okamura and T. Kobayashi, “Octave-spanning carrier–envelope phase stabilized visible pulse with sub-3-fs pulse duration”, Opt. Lett. 36 (2), 226 (2011), doi:10.1364/OL.36.000226 |
| [44] | S. Pekarek et al., “Self-referenceable frequency comb from a gigahertz diode-pumped solid-state laser”, Opt. Express 19 (17), 16491 (2011), doi:10.1364/OE.19.016491 |
| [45] | S. Schilt et al., “Fully stabilized optical frequency comb with sub-radian CEO phase noise from a SESAM-modelocked 1.5-µm solid-state laser”, Opt. Express 19 (24), 24171 (2001), doi:10.1364/OE.19.024171 |
| [46] | G. Marra et al., “Dissemination of an optical frequency comb over fiber with 3 × 10−18 fractional accuracy”, Opt. Express 20 (2), 1775 (2012), doi:10.1364/OE.20.001775 |
| [47] | K. Saha et al., “Modelocking and femtosecond pulse generation in chip-based frequency combs”, Opt. Express 21 (1), 1335 (2013), doi:10.1364/OE.21.001335 |
| [48] | D. Burghoff, “Terahertz laser frequency combs”, Nature Photon. 8, 462 (2014), doi:10.1038/nphoton.2014.85 |
| [49] | D. Nicholodi, “Spectral purity transfer between optical wavelengths at the 10−18 level”, Nature Photon. 8, 219 (2014), doi:10.1038/nphoton.2013.361 |
| [50] | G. Millot et al., “Frequency-agile dual-comb spectroscopy”, Nature Photon. 10, 27 (2015), doi:10.1038/nphoton.2015.250 |
| [51] | A. Klenner et al., “Gigahertz frequency comb offset stabilization based on supercontinuum generation in silicon nitride waveguides”, Opt. Express 24 (10), 11043 (2016), doi:10.1364/OE.24.011043 |
| [52] | J. Kim and Y. Song, “Ultralow-noise mode-locked fiber lasers and frequency combs: principles, status, and applications”, Advances in Optics and Photonics 8 (3), 465 (2016), doi:10.1364/AOP.8.000465 |
| [53] | M. Lezius et al., “Space-borne frequency comb metrology”, Optica 3 (12), 1381 (2016), doi:10.1364/OPTICA.3.001381 |
| [54] | P. Marin-Palomo et al., “Microresonator-based solitons for massively parallel coherent optical communications”, Nature 546, 274 (2017), doi:10.1038/nature22387 |
| [55] | N. Picqué and T. W. Hänsch, “Frequency comb spectroscopy”, Nature Photon. 13, 146 (2019), doi:10.1038/s41566-018-0347-5 |
| [56] | A. Villois et al., “Frequency combs in a microring optical parametric oscillator”, Opt. Lett. 44 (18), 4443 (2019), doi:10.1364/OL.44.004443 |
| [57] | M.-G. Suh and K. Vahala, “Gigahertz-repetition-rate soliton microcombs”, Optica 5 (1), 65 (2018), doi:10.1364/OPTICA.5.000065 |
| [58] | J. Ye and S. T. Cundiff, Femtosecond Optical Frequency Comb Technology, Springer (2005) |
See also: optical frequency, frequency metrology, spectroscopy, optical spectrum, beat note, carrier–envelope offset, mode locking, laser noise, phase noise, optical clocks, optical clockworks, titanium–sapphire lasers, optical heterodyne detection, The Photonics Spotlight 2006-07-01, The Photonics Spotlight 2006-07-01b, The Photonics Spotlight 2006-09-22, The Photonics Spotlight 2007-10-11
and other articles in the categories light pulses, methods
This encyclopedia is authored by Dr. Rüdiger Paschotta, the founder and executive of RP Photonics Consulting GmbH. How about a tailored training course from this distinguished expert at your location? Contact RP Photonics to find out how his technical consulting services (e.g. product designs, problem solving, independent evaluations, training) and software could become very valuable for your business!
 |
If you like this page, please share the link with your friends and colleagues, e.g. via social media:
These sharing buttons are implemented in a privacy-friendly way!