Gaussian Pulses
Definition: pulses with a temporal intensity profile which has a Gaussian shape
More general term: light pulses
German: gaußförmige Pulse
How to cite the article; suggest additional literature
Author: Dr. Rüdiger Paschotta
Ultrashort pulses from mode-locked lasers, for example, often have a temporal shape (i.e., shape of the curve showing optical power versus time) which can be approximately described with a Gaussian function:
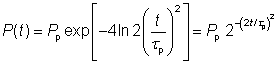
where τ is the full width at half-maximum (FWHM) pulse duration.
In many cases, Gaussian pulses have no chirp, i.e., are transform-limited. In that case, the spectral width (optical bandwidth) is
which means that the time–bandwidth product is ≈ 0.44.
Compared with a sech2-shaped pulse, a Gaussian pulse with the same width at half-maximum has somewhat weaker wings:
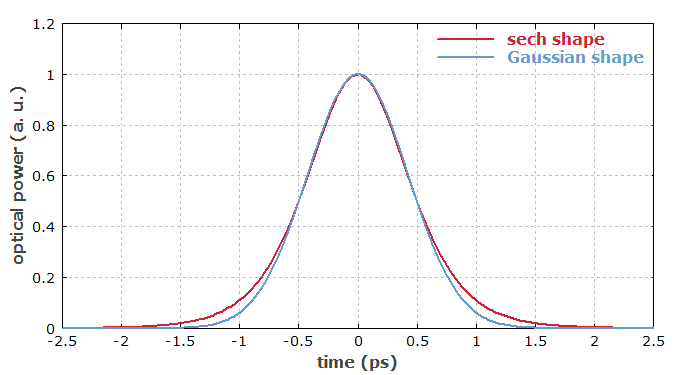
The peak power of a Gaussian pulse is ≈ 0.94 times the pulse energy divided by the FWHM pulse duration.
The Gaussian pulse shape is typical for pulses from actively mode-locked lasers; it results e.g. from the Haus master equation in simple cases. However, it is also found in various other situations.
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here; we would otherwise delete it soon. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
See also: pulses, transform limit
and other articles in the category light pulses
 |




If you like this page, please share the link with your friends and colleagues, e.g. via social media:
These sharing buttons are implemented in a privacy-friendly way!