Passive Fiber Optics

In principle, a fiber with a fully rotationally symmetric design should have no birefringence. It should thus fully preserve the polarization of light. In reality, however, some amount of birefringence always results from imperfections of the fiber (e.g., a slight ellipticity of the fiber core), or from bending. Therefore, the polarization state of light is changed within a relatively short length of fiber – sometimes only within a few meters, sometimes much faster.

Note that the index difference between polarization directions is not necessarily larger in fibers than in other devices. However, fibers tend to be long, so that even weak index differences can have substantial effects.

Another important aspect is that the resulting polarization changes are not only random and unpredictable, but also strongly dependent on the wavelength, the fiber's temperatures along its whole length, and on any bending of the fiber. Therefore, it often doesn't help that much to adjust a polarization state, e.g. using a fiber polarization controller (see below); some slight changes of environmental parameters or wavelength may again spoil the polarization.

Strong bending of a fiber introduces birefringence. This means that some appropriate length of fiber, bent with a certain radius and fixed on a coil, can have a relative phase delay of π, or π/2, for example, between the two polarization directions. It can thus act like a λ/2 waveplate (half-waveplate) or a λ/4 waveplate (quarter-waveplate). If one rotates the whole coil around an axis which coincides with the incoming and outgoing fiber, one obtains a similar effect as for rotating a bulk waveplate in a free-space laser beam. One often uses a combination of an effective quarter-waveplate coil with a half-waveplate coil and another quarter-waveplate coil in series to transform some input polarization state into any wanted polarization state. Such a fiber polarization controller (Figure 1) can work over some substantial wavelength region.

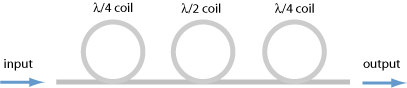
As mentioned before, the problem may remain that the input polarization state drifts with changing environmental conditions, so that the fiber polarization controller would have to be realigned frequently in order to preserve a constant output polarization state.

Fibers can be made polarization-maintaining (PM fiber) – but not by avoiding any birefringence! To the contrary, one intentionally introduces a significant birefringence. Such fibers are thus high-birefringence fibers (HIBI fibers).

There are essentially two common ways for doing that:

• A fiber can be made with an elliptical core. This results in some level of form birefringence. Of course, the fiber modes will also be affected by the elliptical shape, and the efficiency of coupling light to or from fibers with circular core is somewhat reduced.
• Some mechanical stress can be applied, e.g. by introducing stress rods made from a different glass. See Figure 2 for some typical realizations.

Note: a polarization-maintaining fiber does not preserve any polarization state of injected light! It does so only for linearly polarized light, where the polarization direction must be one of two orthogonal directions, e.g. along a line between the stress rods or perpendicular to it. The β value for some wavelength will significantly depend on that polarization direction.

What happens if we inject monochromatic with some other linear polarization direction? That can be considered as a superposition of the two basic polarization states. After a short length of propagation, these components will have acquired significantly different phase delays (due to their different β values). Therefore, they will no longer combine to the original linear polarization state, but rather in general to some elliptical state. After integer multiples of the polarization beat length, however, one again obtains a linear polarization.

For non-monochromatic light, the situation becomes even more complicated. Over some length of fiber, the different wavelength components will experience different polarization-dependent phase shifts, so that the resulting polarization state becomes wavelength-dependent. To convert that back into a linear state would be difficult task – a simple polarization controller could not do that.

The need to align the input polarization state to a fiber axis in order to have the polarization preserved is of course a serious practical disadvantage of PM fibers. It requires more work to fabricate PM fiber-optic setups, for which additional equipment is required. Also, not all fiber components are available as PM versions. On the other hand, detrimental effects of drifting polarization states, which may otherwise require other measures, are safely avoided with PM setups.

Note that the introduced birefringence essentially removes any effect of some small additional random birefringence, as can result from moderate bending, for example. Such random influences may only very slightly change the local polarization, but will normally not have any significant effect on longer lengths. One can understand this by considering mode coupling: significant mode coupling requires a perturbation which has a period equal to the beat period of the two polarization states. For strong birefringence, that beat period (the polarization beat length) is rather short (for example, a few millimeters), and the usual perturbations are spatially too “slow” to cause any significant coupling, or at least do not have a strong spatial Fourier component according to the polarization beat.

Another way of eliminating polarization issues is to design devices such that polarization does not matter. This approach is usually taken in optical fiber communications, for example. One simply takes care that no components are used which could cause substantial polarization-dependent losses, or which would rely on a certain polarization state. For example, one generally cannot use electro-optic modulators, and needs to carefully design any semiconductor devices for low polarization dependence. Some polarization effects still remain, which may limit the performance of very fast fiber-optic links. In particular, there is the phenomenon of polarization mode dispersion (PMD), which may be quantified as a differential group delay (DGD): signal components with different polarization may require slightly different times for traveling through a fiber cable, and that may deteriorate the signal quality. For short transmission distances and/or moderate bit rates, however, PMD is not a big issue.

Go to Part 10: Chromatic Dispersion of Fibers or back to the start page.

Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.

Please do not enter personal data here; we would otherwise delete it soon. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him e.g. via e-mail.