Color Spaces

The LMS color space is defined based on three coordinates L, M and S, each one measuring the strength of excitation of one of the three types of cones in the retina of the human eye. Note that it is physically not possible e.g. to have a non-zero M value combined with L and S being zero, because the spectral response curves of the three receptors are substantially overlapping. Therefore, the range of perceivable colors corresponds to a volume in LMS color space which is not simply a cuboid.

For monochromatic light, the L, M and S values are defined by the LMS color matching functions of CIE, see Figure 1. These data can of course also be applied to polychromatic light, integrating the contributions of different wavelength components according to some optical spectrum.

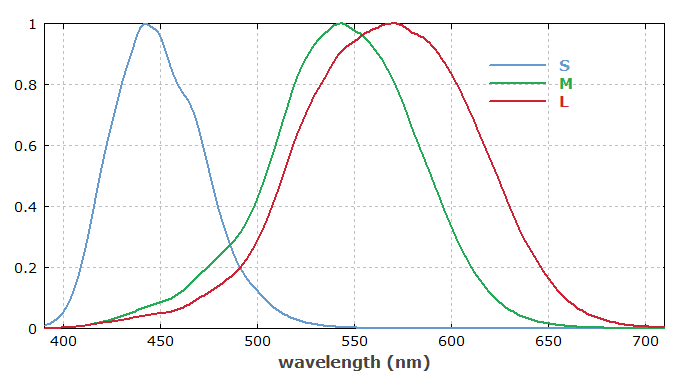
LMS values can be directly measured e.g. in a tristimulus colorimeter and are useful e.g. for comparing color values: two different optical spectra having the same LMS coordinates can be expected to create the same color impression, at least for human beings with normal color vision.

LMS color space can represent any perceivable colors. However, it is not particularly suitable for some technical applications. In particular, it is not immediately apparent how to generate light which creates the color impression related to a particular point in LMS color space; we cannot directly address the different receptors in the eye, because of their spectral sensitivity curves overlap substantially.

In 1931, the CIE (Commission Internationale de l'Éclairage = International Commission on Illumination) has defined its XYZ color space, which has become very important; it has become a general reference and the basis for the definition of various other color spaces.

The CIE color model takes the luminance (as measure for perceived brightness) as one of the three color coordinates, calling it Y. The spectral response of the luminance is specified as the photopic luminosity function. The maximum possible Y value, e.g. for a color image, may be chosen to be 1 or 100, for example. The coordinate Z responds mostly to shorter-wavelength light, while X responds both to shorter- and longer-wavelength light. Figure 2 shows the used color matching functions.

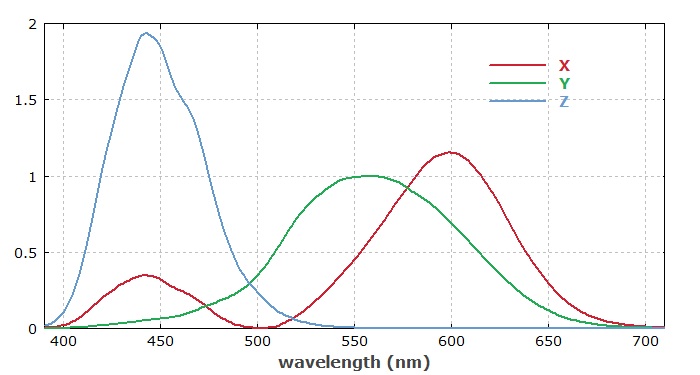
CIE has also introduced normalized coordinates x, y and z, obtained by dividing the X, Y and Z values by (X + Y + Z). One can then take x and y as chromaticity coordinates, determining color tones for a certain luminance. That system is called CIE xyY, because a color value is defined by the chromaticity coordinates x and y in addition to the luminance coordinate Y.

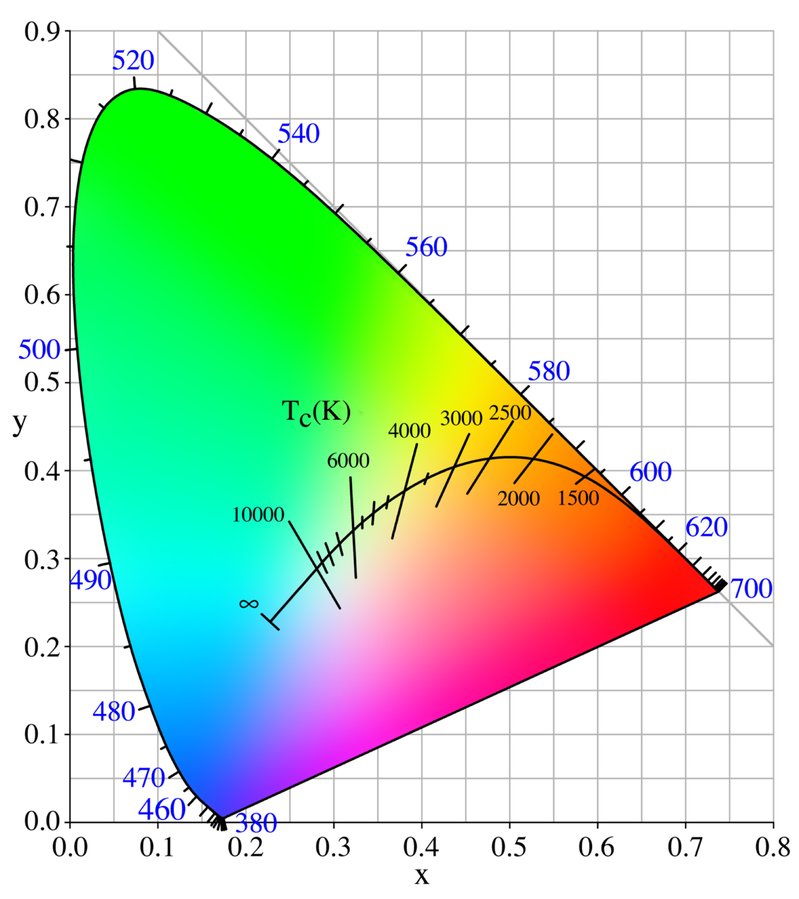
The CIE chromaticity diagram (Figure 3) would ideally display the true color tones for all x, y pairs in the perceivable range of colors, which corresponds to a horseshoe-shaped part of XYZ color space, called the gamut of human vision. Unfortunately, a computer monitor can display colors only in a limited part of the XYZ color space, e.g. the sRGB color space (see below), and even in that limited space the colors may not be accurate if one does not take special precautions, such as a careful color calibration according to the color space of the displayed image. Therefore, such CIE chromaticity diagrams, whether printed on paper or displayed on a screen, are usually showing colors only in quite approximate ways. A rather accurate reproduction could in principle be done with a laser-based display employing carefully controlled mixtures of several primary colors, e.g. deep red at 700 nm, green at 530 nm, blue-green at 500 nm and blue-violet at 480 nm. That would go substantially beyond the color limitations of displays with RGB sources (using three primary colors), but would also be correspondingly more complex and expensive, and is therefore not common.

The primary colors of CIE XYZ color space (e.g. with X = 1, Y = Z = 0) are imaginary colors, i.e., they cannot be physically realized. Colors for monochromatic light are located on the spectral locus of the chromaticity diagram, which is the curved boundary of the shown gamut; wavelength values in nanometers are indicated in Figure 3. The lower boundary of the gamut, called the line of purples, basically represent some mixtures of red and violet, which cannot be reached with monochromatic light.

White light with a flat power spectrum (CIE standard illuminant E) corresponds to the point with x = y = 1/3. In real life, one may encounter different white color tones like warm white (somewhat shifted towards yellow-orange), cold white (with higher blue content), etc. Figure 3 also shows the color values of blackbody radiation (thermal radiation with spectrally uniform emissivity) for a range of temperatures.

Note that distances in CIE XYZ color space do not well reflect differences in perceived color tones; that deficiency of the system has led to the development of various other color spaces such as CIELUV, CIEUVW, and CIELAB, which are better in that respect and others. Relatively common e.g. for-color calculations is CIELAB (L*a*b*) with a luminance coordinate L* and two chromaticity coordinates a* (green to magenta) and b* (blue to yellow).

On computer monitors and projection displays with RGB sources, colors are usually obtained by additive mixing of red, green and blue light. For example, these may be emitted by different phosphors of a cathode ray tube (CRT) or by light-emitting diodes, or obtained with a suitable optical filters from an LED background light or a high intensity discharge lamp. For such applications, it is obviously convenient to have colors defined with RGB (red–green–blue) coordinates, i.e., in an RGB color space. One may then directly control the red, green and blue intensities according to the color coordinates, or sometimes first needs to apply a transformation.

In principle, one may also work with a different set of colors, but with a combination of red, green and blue one can best produce a reasonably large color gamut.

The RGB color model defines only the basic principle; one also needs to define the exact primary colors and some other details (e.g. a gamma function). There is a substantial number of different RGB color spaces:

• The sRGB color space, defined by HP and Microsoft, was originally designed to work well with cathode ray tube displays. The phosphors which are typically used in those (with substantially non-monochromatic emission) substantially limit the color gamut. Deficiencies are particularly apparent in the blue-green region, but a deep red is also not included. Typical CMYK spaces (see below) are largely, but not completely covered. Despite its limitations, the sRGB color space is still very widely used and often considered to be the default if the color space of an image is not explicitly specified. Flat panel liquid crystal displays, e.g. with LED-based backlight, often achieve a quite similar color gamut, so that the use of sRGB is still appropriate. That is not the case, however, for monitors with substantially expanded color gamut, which are used for example in applications like print productions and arts, sometimes also for video viewing. Photo cameras also often deliver sRGB image data, e.g. in JPG files.
• Adobe RGB is using a substantially wider color gamut, extended against sRGB in the green region. A later version is Adobe Wide Gamut RGB, having a further extended color gamut. Such versions are preferable for applications requiring a wider range of colors.
• CIE 1931 RGB is a rather early version, using a set of monochromatic primary colors (700 nm, 546.1 nm and 435.8 nm). It is a comparatively wide color gamut, which could actually be even much wider if a green color with shorter wavelength (e.g. 515 nm) would be used. However, this place cannot be directly used for RGB displays, because those can usually not realize the required monochromatic primary colors.

Note that mathematically one can cover the complete gamut of human vision with RGB coordinates, if one allows those to become negative. However, a pixel of a color monitor cannot contribute less than no green light at all, for example, although that would be required to generate color impressions in the deepest red region. Usually, one considers only non-negative RGB values, corresponding to colors which can physically be generated by mixing the used primary colors.

Devices using RGB color profiles are often equipped with a color profile (most often based on a definition from ICC, the International Color Consortium), which essentially defines more closely the used primary colors. One may, for example, use a colorimeter to generate a color profile of a computer monitor; the resulting file can then be used for properly adjusting the color values, e.g. such that the RGB color space of available media is accurately reproduced. Also, a photo camera my embed its color profile into produced JPEG images files in order to clearly define what color space has been used.

CMYK color spaces are based on a subtractive color model, as is appropriate in the context of printing, where colors are generated by mixing pigments or dyes. Here, each segment absorbs light in some range of wavelengths. CMYK values essentially specify what concentrations of C (cyan), M (magenta), Y (yellow) and K (black) pigments or dyes (e.g. in ink jet printers) need to be mixed to obtain the corresponding color. Although human vision is trichromatic, meaning that three different pigments would in principle be sufficient, a combination of four has been chosen to obtain a wider color gamut. Nevertheless, CMYK color gamuts are relatively narrow, with substantial deficiencies particularly in the blue–green region, but also for deep red color tones. This reflects the fundamental difficulties of achieving such colors with pigments. If a pigment were to generate a very “pure” color (close to some monochromatic light), it would have to absorb all light outside a narrow wavelength band, and leave only a tiny portion of the incident optical power. However, for subtractive color mixing to work reasonably well, one needs to have substantially overlapping spectral regions with low absorption, and that inevitably leads to broadband light with quite limited color saturation.

Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.

Please do not enter personal data here; we would otherwise delete it soon. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him e.g. via e-mail.