RP Resonator – das Software-Werkzeug für Design und Optimierung von Laserresonatoren
| Überblick | Anwendung | Modell | Benutzung | Demos | Versionen |
Beispiel: Titan-Saphir-Laser
Wir betrachten einen modengekoppelten Titan-Saphir-Laser, wobei der Laserresonator ein Prismenpaar für die Dispersionskompensation enthält. Der Resonatoraufbau:
diagram 1, size_px = (600, 280): "Resonator Setup" draw resonator, direction = 2 * th1 ["a = ", a:d3:"m"], 400, 500 ["b = ", b:d3:"m"], 400, 550 ["d = ", d:d3:"m"], 400, 600 ["e = ", e:d3:"m"], 400, 650 ["f = ", f:d3:"m"], 400, 700 ["g = ", g:d3:"m"], 400, 750 ["h = ", h:d3:"m"], 400, 800 ["R1 = ", R1:d3:"m"], 600, 500 ["R2 = ", R2:d3:"m"], 600, 550 ["R3 = ", R3:d3:"m"], 600, 600 ["f_rep = ", f_rep:d3:"Hz"], 600, 650 ["GDD = ", GDD / 1e-15^2:f0:"fs^2"], 600, 700 ["tau_soliton = ", tau_soliton:d3:"s"], 600, 750 ["S_SESAM = ", S_SESAM:d3], 600, 800
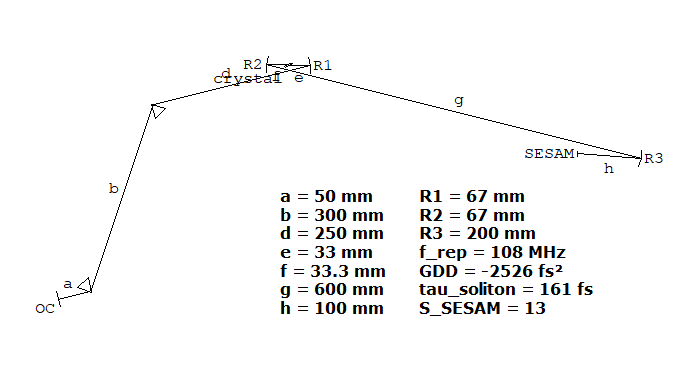
Hier wurden einige berechnete Resonatorparameter wie Armlängen und Krümmungsradien von Spiegeln angezeigt, ebenfalls einige berechnete Resonatoreigenschaften wie die chromatische Dispersion und die erwartete Solitonen-Pulsdauer. Die Dispersion (GDD =group delay dispersion) wird von der Software automatisch berechnet, während die erwartete Solitonen-Pulsdauer mit einigen Skriptzeilen (hier nicht gezeigt) berechnet wird, welche auf berechnete Eigenschaften wie z. B. die Modenfläche im Laserkristall und auf zusätzliche Angaben (z. B. die erwartete durchschnittliche Ausgangsleistung) zugreifen. Durch die Möglichkeit, diverse benutzerdefinierte berechnete Größen anzuzeigen, können Sie RP Resonator nicht nur für das eigentliche Resonatordesign einsetzen, sondern oft sogar für das Design des gesamten Lasersystems. Beispielsweise lassen sich Aspekte wie die Pulsformung durch Q switching oder mode locking gleich mit berücksichtigen. Man erspart sich dann den Wechsel zwischen verschiedenen Programmen zur Behandlung verschiedener Aspekte.
Nun plotten wir den Strahlradius als Funktion der Position im Resonator:
diagram 2: "Beam Radius vs. Position" x: 0, L_res / cm "z position (cm)", @x, font = Arial, size = %5 y: 0, 1500 "beam radii (µm)", @y, font = Arial, size = %5 legpos 500, 120, size = %4 frame hx hy f: w_t(x * cm, lambda_ref) / um, "tangential direction", color = lightred, width = 3, step = 1 f: w_s(x * cm, lambda_ref) / um, "sagittal direction", color = lightblue, width = 3 "OC", (0)l, (w_t(0, lambda_ref) / um)b "R1", (zm[M1] / cm)c, (w_t(zm[M1], lambda_ref) / um)b "R2", (zm[M2] / cm)c, (w_t(zm[M2], lambda_ref) / um)b "R3", (zm[M3] / cm)c, (w_t(zm[M3], lambda_ref) / um)b
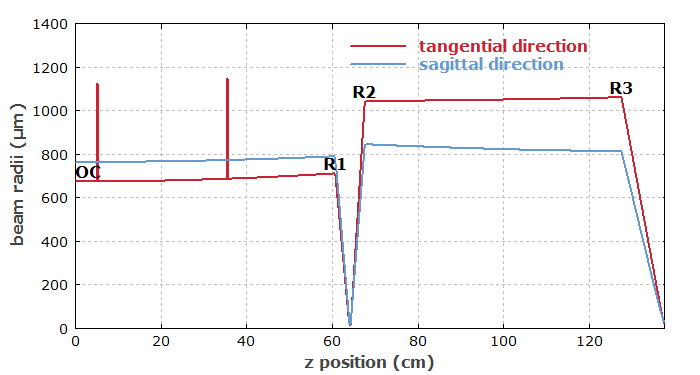
Als nächstes zeigen wir die Strahlradius an verschiedenen Stellen als Funktionen der Armlänge e:
diagram 3:
"Beam Radii versus Length e"
x: 3.2, 3.6
"length e (cm)", @x
y: 0, 100
"beam radii (µm)", @y
legpos 500, 120, size = %4
frame
hx
hy
! e0 := e { save original value }
f: (Init (e := x * cm); w(zm[crystal], lambda_ref) / um),
maxconnect = 0.2, step = 3, "w(crystal)", color = black, width = 3
f: (Init (e := x * cm); w(zm[OC], lambda_ref) / um) / 10,
maxconnect = 0.4, step = 3, "w(OC) / 10", color = lightblue, width = 3
f: (Init (e := x * cm); w(zm[SESAM],lambda_ref) / um),
maxconnect = 0.4, step = 3, "w(SESAM)", color = lightred, width = 3
f: (Init (e := x * cm); abs(dx(zm[crystal], lambda_ref)) / um),
maxconnect = 0.4, step = 3, "|dx(crystal)|", style = dotted, width = 3
! Init(e := e0) { restore original value }
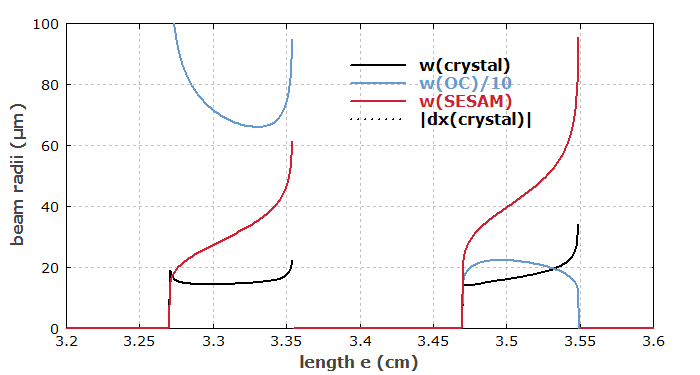
Die gestrichelte Kurve zeigt die Strahlverschiebung, die von einer leichten Fehljustage des Auskoppelspiegels verursacht wird. Dies gibt Informationen über die Justageempfindlichkeit, die am rechten Ende der ersten Stabilitätszone divergiert.
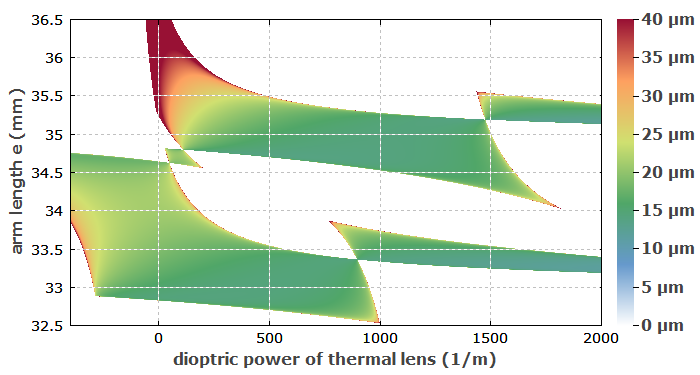
Schließlich erzeugen wir einen 2D-Plot, der den Strahlradius im Laserkristall als Funktion der Brechkraft und der Armlänge e zeigt. Die etwas überraschende Form rührt daher, dass an einigen Stellen des Diagramms ein starker Astigmatismus auftritt.