Fizeau Interferometers

One exploits interference between reflections at a test surface and a nearby reference surface, as shown in Figure 1. The reference surface in Figure 1 is the right surface of an optical flat, having a particularly high flatness and also otherwise high surface quality. Normally, the reference surface is slightly tilted (e.g. controlled with a micrometer screw) against the tested surface, so that for ideal surface quality one would obtain a regular pattern of straight interference fringes (stripes). Any deviations between the surface shapes lead to distortions of those stripes (Fizeau curves).

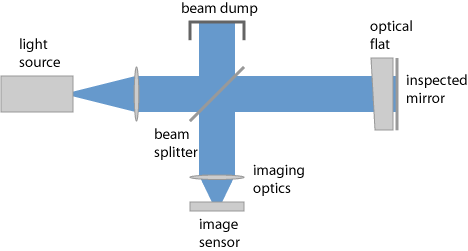
The tested surface does not need to be highly reflective; its reflectivity should just be high enough to produce a clear interference pattern.

Influences of reflections from the left side of the optical flat may be minimized with an anti-reflection coating, with a wedge shape of the optical flat and in addition sometimes exploiting the limited coherence length of the used light.

The used light source can be a laser, but one can also use other light sources such as gas discharge lamps. The light does not need to be highly monochromatic if the distance between the test surface and the reference surface is small.

A Fizeau interferometer can be seen as a simpler alternative to a Twyman–Green interferometer. Its advantage is that interference occurs only between two closely spaced parts, and only the relative distance of those last be carefully controlled. The orientation of the beam splitter, for example, is not critical. On the other hand, the Twyman–Green interferometer is more flexible, for example concerning the optimization of fringe contrast for different reflectivities of the investigated samples.

There is also a similarity to a Fabry–Pérot interferometer. The Fizeau interferometer can be considered as a Fabry–Pérot interferometer made for surface characterizations. Typically, it does not exhibit sharp resonances due to low surface reflectivities.

Your question or comment:

Spam check:

  (Please enter the sum of thirteen and three in the form of digits!)

By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.

[1]	Y. H. Meyer, “Fringe shape with an interferential wedge”, J. Opt. Soc. Am. 71 (10), 1255 (1981), doi:10.1364/JOSA.71.001255
[2]	T. T. Kajava, H. M. Lauranto, and A. T. Friberg, “ Interference pattern of the Fizeau interferometer”, J. Opt. Soc. Am. A 11 (7), 2045 (1994), doi:10.1364/JOSAA.11.002045

(Suggest additional literature!)