
RP Fiber Power – Simulation and Design Software
for Fiber Optics, Amplifiers and Fiber Lasers
| Overview | Features | Speed | Model |
| Data | Interface | Demos | Versions |
Example Case: Stimulated Raman Scattering in Yb-doped Fiber Amplifier
Description of the Model
Here, we simulate the propagation of an ultrashort pulse in a fiber amplifier, where the substantial fiber nonlinearity leads to stimulated Raman scattering (SRS). The model is similar to that for parabolic pulse propagation, except that the fiber is longer and the pulse parameters are different.
Results
Figure 1 shows the amplified pulse in the time domain. Particularly in the leading part, it exhibits fast wiggles. These result from the interference of the original part of the pulse spectrum with the Raman-shifted part.
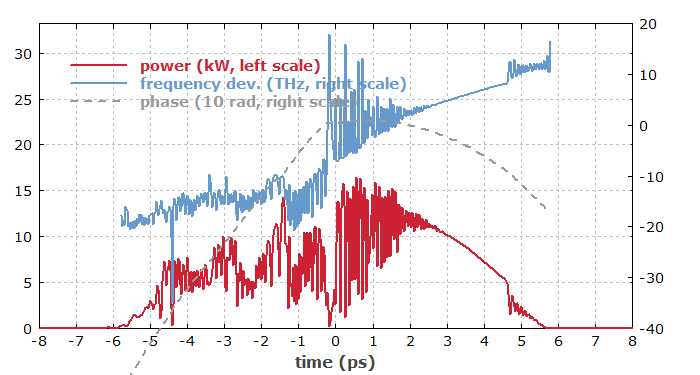
Figure 2 shows the pulse spectrum. (For comparison, the narrow spectrum of the input pulse at 1040 nm is shown with a dotted curve, with the energy increased by a factor of 30.) Much of the pulse energy has been shifted to the long-wavelength region around 1080–1120 nm. Note that subsequent simulation runs deliver somewhat different structures in that part due to the randomness of Raman scattering, which is influence by quantum fluctuations.
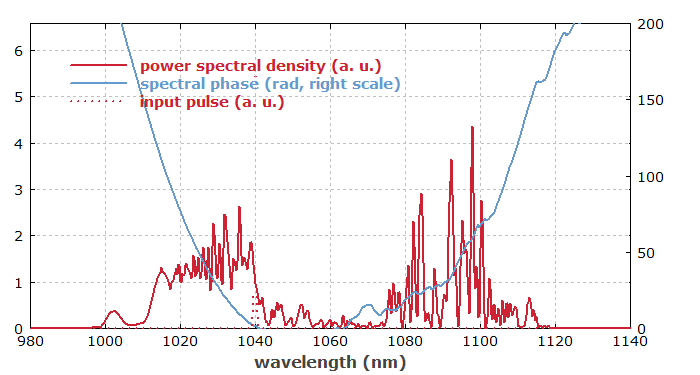
Figure 3 shows the spectrogram of the output pulse. The original component shows an up-chirp due to the normal chromatic dispersion of the fiber, whereas the Raman-shifted part exhibits an irregular structure.
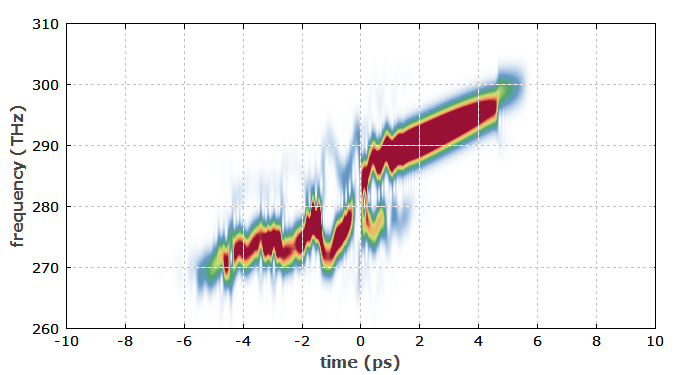
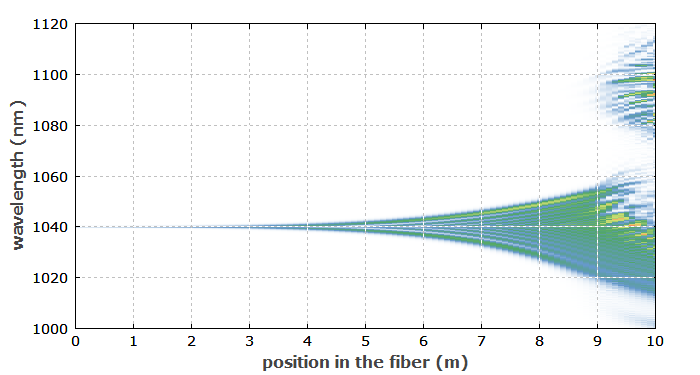
Figure 4 shows how the pulse spectrum evolves in the fiber. Towards the right side, it first gets broader and broader (mainly due to self-phase modulation), and in the last part, the Raman scattering effect sets in. One can see how it “eats up” particularly the longer-wavelength part of the original spectral region. This is because the shorter-wavelength components propagate with a somewhat lower speed, losing the temporal overlap with the Raman-shifted part. (For a similar reason, one can see in Figure 1 that the trailing part of the pulse in the time domain is not affected by SRS.)
Note that the detailed behavior of the pulses depends substantially on various parameters. For example, for femtosecond pulses, having a broader spectrum, Raman spectrum can occur within the spectrum. This strongly reduces the impact of quantum fluctuations; the pulse propagation becomes much more deterministic. In other cases, the chromatic dispersion is different, which can also substantially change the results.
