RP ProPulse – Simulation der Ausbreitung ultrakurzer Pulse
| Überblick | Anwendung | Modell | Benutzung | Demos | Versionen |
Beispiel: Aktives Modenkoppeln
In diesem Beispiel betrachten wir einen aktiv modengekoppelten Laser. Der Laserresonator wird im Skript wie folgt beschrieben:
resonator: ring * Crystal: gain(l) = g(l) [P_sat_av = P_sat_g, KK = 0] * Modulator: mod(t) = t_mod(t) * OC: T_out = T_OC resonator end
Hier wird auf einige Variablenwerte zurückgegriffen, deren Definitionen hier nicht gezeigt sind. Die Gain-Funktion g(l) hat eine begrenzte Bandbreite von 0,2 nm, und der Modulator moduliert die Umlaufverluste mit 100 MHz und maximalen Verlusten von 10 %.
Die anfängliche Pulsdauer wurde etwas länger als im stationären Zustand gewählt. Man findet, dass der stationäre Wert der Pulsdauer mit dem Wert der Kuizenga-Siegman-Theorie übereinstimmt (siehe das Diagramm).
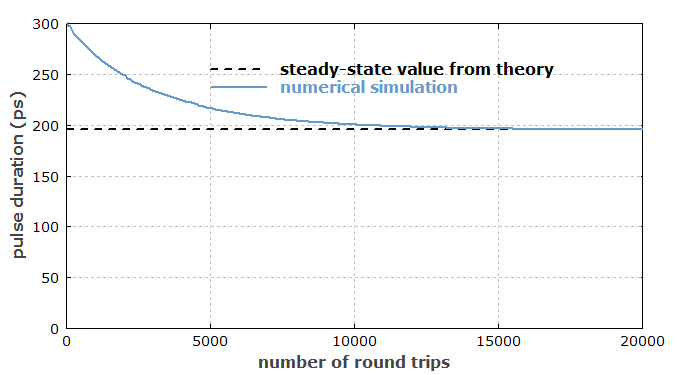
Der Skriptcode für dieses Diagramm ist ziemlich einfach:
; ---------------------------
diagram 1:
"Evolution of Pulse Parameters"
x: 0, 20000
"number of round trips", @x
y: 0, 300
"pulse duration (ps)", @y
frame
legpos 200, 160
hx
hy
tau_th := 0.45 * ((0.5 * T_OC) / (0.25 * A_mod))^0.25 / sqrt(f_mod * df_g)
{ theoretical value for steady-state pulse duration
according to Kuizenga-Siegman theory }
f: tau_th / ps,
"steady-state value from theory",
style = dashed, width = 3
f: (getpulse(x / rt_per_step,0); tau()) / ps,
"numerical simulation", color = blue, width = 3
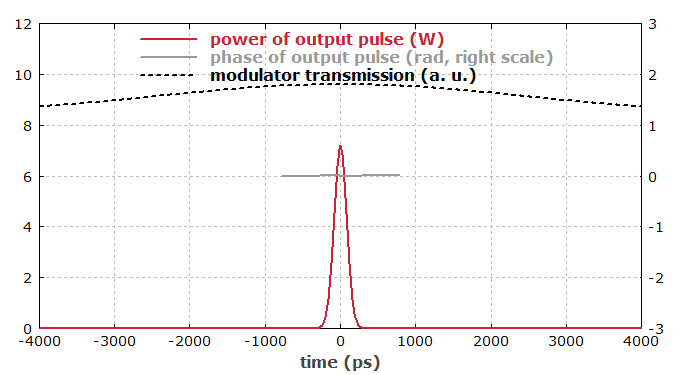
Wir können ebenfalls das zeitliche Profil nach 2000 Resonatorumläufen anzeigen (die auf einem gewöhnlichen PC in wenigen Sekunden berechnet sind):