Object and Image Space
Definition: mathematical spaces for the description of optical elements and systems
German: Objekt- und Bildraum
Categories: general optics, vision, displays and imaging
How to cite the article; suggest additional literature
Author: Dr. Rüdiger Paschotta
In geometrical optics, extensive use is made of the concept of object and image spaces. In the simplest case, an object and image space is associated with a single optical element of zero longitudinal extension – for example, a plane or curved interface between two transparent optical media. In a first approach, one may consider the object space to be the space before that interface and the image space to lie after the interface; one sometimes finds drawings which suggest that. However, it is common practice to consider both object and image space to span the complete space. For example, one can extrapolate any rays on the object side to the image side – without taking into account any changes at the interface – to obtain those rays in the complete object space. Similarly, one can extrapolate back any rays on the image side. By extrapolating convergent rays, which meet in some point, one can obtain virtual points. For example, in image space one may have a virtual image of an object point.
Object space can thus contain real object points before the optical system and virtual object points behind it. Similarly, image space can contain real image points behind the system and virtual image points before it. For example, when using a photo camera, one deals with real object points in front of the camera, which are related to real image points on the film or image sensor.
Figure 1 shows a situation where a biconcave and thus defocusing (negative) lens modifies the appearance of a real object: on the image side, the rays appear to come from a virtual object position, and that is part of image space despite lying left of the lens. On the other hand, object space contains the rays coming from the object, not affected by the lens.
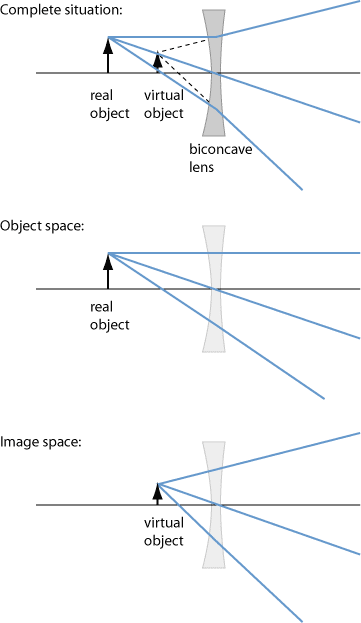
A similar situation would be found for a magnifying glass, where a focusing lens is used.
One can easily apply the concept of object and image space to extended optical systems, consisting of multiple optical elements.
In drawings, one often shows items of object and image space together (as in the top part of Figure 1). In order to avoid confusion in drawings or text, one may use some appropriate system of labeling. For example, one may indicate all points with capital letters, adding a prime for all points and image space only.
An optical imaging system will never be able to image all points of object space. It is not only that object space also comprises points behind the system, but also that there are limitations to the locations from which points before the system can be imaged. In particular, there is a limited field of view, and in addition there are usually limitations for sharp imaging; for example, one may not be able to focus a camera on very close objects.
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here; we would otherwise delete it soon. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.
See also: geometrical optics
and other articles in the categories general optics, vision, displays and imaging
 |



If you like this page, please share the link with your friends and colleagues, e.g. via social media:
These sharing buttons are implemented in a privacy-friendly way!