RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: Stimulierte Raman-Streuung in einer Multimode-Faser
Beschreibung des Modells
Wir nehmen hier an, dass Pumplicht bei 1550 nm und Signallicht bei 1660 nm in eine Multimode-Faser geschickt werden. Sie haben relativ hohe optische Leistungen von 8 kW bzw. 200 W, was im Falle von Nanosekundenpulsen durchaus realistisch ist. Bei solchen Leistungen erhält man eine starke Raman-Wechselwirkung bereits innerhalb einer Faserlänge von nur 200 mm.
Die Multimode-Faser hat ein parabolisches Brechungsindexprofil. Wir nehmen an, dass der nichtlineare Index und der Raman-Gain-Koeffizient ähnliche transversale Profile aufweisen, da diese Werte normalerweise durch Dotierungen im Faserkern, die den Brechungsindex erhöhen sollen, ebenfalls erhöht werden. Die angenommenen transversalen Profile dieser Eingabewerte werden in Abbildung 1 gezeigt.
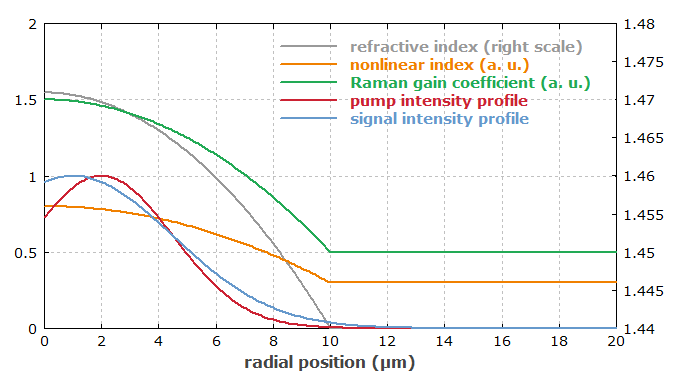
Für die Pump- und Signalstrahlen nehmen wir Gauß-Profile an, die beide ein wenig gegenüber der Mitte des Faserkerns versetzt sind. Sie sind nicht auf bestimmte Fasermoden angepasst. Deshalb regen wir mehrere Pump- und Signalmoden an, die dann miteinander wechselwirken.
Da wir im Modell die transversalen Profile berücksichtigen müssen, verwenden wir die Methode der numerischen Strahlpropagation. Seit 03/2017 kann stimulierte Raman-Streuung in solchen Simulationen berücksichtigt werden. Man könnte dabei übrigens nicht nur eine Pump- und Signalwelle haben, sondern mehrere Wellenlängenkomponenten, die miteinander wechselwirken. Der Raman-Gain-Koeffizient kann einerseits von der optischen Frequenzdifferenz der involvierten Lichtstrahlen abhängen und andererseits von den transversalen Koordinaten. Ebenfalls könnte man in einem solchen Modell einfach auch beliebige Biegungen der Faser berücksichtigen.
Ergebnisse
Abbildung 2 zeigt die Entwicklung der optischen Leistung in der Faser – nicht nur die gesamten Leistungen von Pump- und Signalwelle, sondern auch die Signalleistungen in einigen wichtigen Fasermoden.
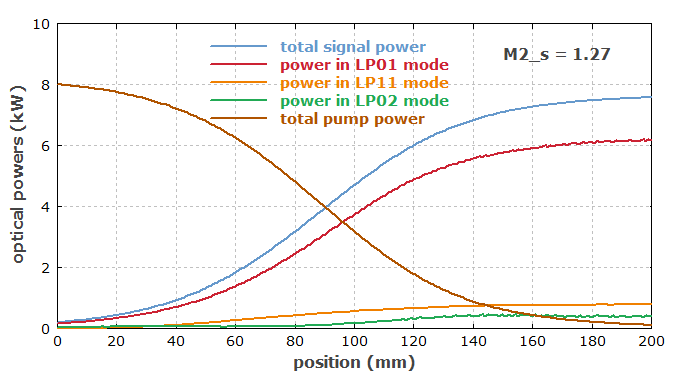
Es könnte erstauen, dass das Verhältnis von ausgehender Signalleistung zu eingehender Pumpleistung größer ist, als es vom Verhältnis der Photonenergien her möglich sein sollte. Man beachte jedoch, dass eine gewisse Signal-Eingangsleistung (200 W) vorliegt. Die Zunahme der Signalleistung ist konsistent mit der Erhaltung der Photonenzahl.
Obwohl die numerische Strahlpropagation als solche nicht auf dem Konzept der Fasermoden beruht, können wir die Leistungen in spezifischen Moden an jeder Stelle in der Faser mit einem Überlappintegral berechnen, welches die jeweilige Modenfunktion enthält. Letztere können wir mit dem eingebauten Mode Solver berechnen. Die folgende Funktion wurde für die Berechnung dieser Leistungen definiert:
P_lm_s(l, m, z) :=
{ signal power in LP_lm mode at position z }
abs2(int(int(bp_A%(x, y, z) * A_lm_xy(l, m, l_s, x, y),
x := -r_max to +r_max step dr),
y := -r_max to +r_max step dr))
Im obigen Diagramm wird auch der M2-Faktor des erhaltenen verstärkten Signalstrahls angezeigt (genau genommen der Mittelwert für x- und y-Richtung). Für diesen Zweck kann man einfach die Funktionen bp_M2_x() und bp_M2_y() verwenden.
Die Berechnungen benötigen auf einem gewöhnlichen Büro-PC rund eine Minute. Beachten Sie, dass man die Amplitudenprofile in einer solchen Faser mit einer recht kleinen numerischen Schrittweite propagieren muss – in unserem Fall ist sie 2 μm, sodass wir insgesamt 100 000 numerische Schritte brauchen. Jeder davon beinhaltet 2D-Fourier-Transformationen und andere aufwendige Berechnungen. Eine einfache Leistungs-Propagation (ohne Berücksichtigung transversale Profile) wäre weitaus weniger rechenaufwendig, ist aber nicht geeignet, um diverse interessante Details des Konversionsprozesses untersuchen zu können.
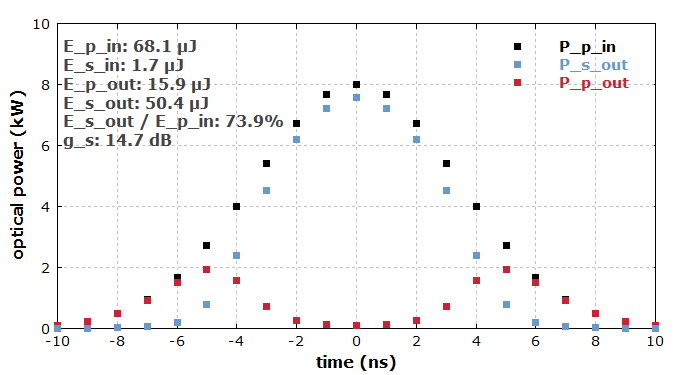
Man kann dieses Modell leicht so weiterentwickeln, dass es die Propagation nicht nur für eine bestimmte Pump- und Signalleistung vornimmt, sondern für etliche Werte entlang eines Pump- und Signalpulses. Hier haben wir angenommen, dass Pump- und Signalpulse 8 ns lang sind, zeitlich übereinstimmen und Peak-Leistungen von 8 kW bzw. 200 W haben. Die Propagation wird durchgeführt mit einer Schrittweite von 1 ns, und die Ausgangsleistungen wurden integriert, um die gesamten Energien und die Konversionseffizienz zu berechnen. Abbildung 3 zeigt die Resultate. Man kann sehen, dass die Raman-Konversion in den zeitlichen Ausläufern der Pulse nicht effizient ist, so dass die gesamte Konversionseffizienz für einen Puls deutlich tiefer liegt als diejenige für das Pulsmaximum.