RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: Superkontinuum-Erzeugung
Beschreibung des Modells
Hier simulieren wir numerisch die Superkontinuumerzeugung in einer Germanosilikatfaser. Die Faser wurde so gestaltet, dass die Wellenlänge mit verschwindender chromatischer Dispersion nicht weit von der Pumpwellenlänge von 1550 nm entfernt ist, da dies eine bessere spektrale Verbreiterung ermöglicht. Der mode solver wurde benutzt, um die effektive Modenfläche und die chromatische Dispersion aus dem gegebenen Brechungsindexprofil zu berechnen. Die Wellenlängenabhängigkeit der Brechungsindizes wird mit Hilfe von Sellmeier-Gleichungen berücksichtigt.
Pulse mit 1 nJ Energie und 400 fs Dauer werden in die Faser geschickt. Die Superkontinuumerzeugung involviert ein kompliziertes Zusammenspiel von Nichtlinearität und Dispersion in der Faser. Betreffend die Nichtlinearität muss nicht nur der Kerr-Effekt berücksichtigt werden, sondern auch Ramanstreuung und self-steepening. Das volle Profil der chromatischen Dispersion wird direkt vom mode solver übernommen. Die integrierte automatische Schrittweitenkontrolle ist nützlich, da gegen Ende der Faser wesentlich feinere numerische Schritte benötigt werden, um eine gute Genauigkeit zu erhalten.
Ergebnisse
Abbildung 1 zeigt die die wellenlängenabhängige Gruppengeschwindigkeitsdispersion und den Gruppenindex der Faser. Beides wurde aus dem Brechungsindexprofil berechnet. Man erkennt, dass die Wellenlänge mit veschwindender Dispersion bei ca. 1500 nm liegt, nicht weit von der Pumpwellenlänge (1550 nm).
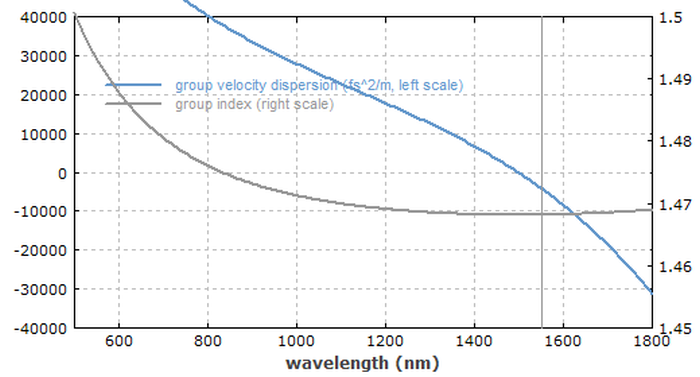
Abbildung 2 zeigt den erhaltenen Puls in der zeitlichen Domäne. Der Anfang des Pulses wurde nicht stark verändert, der Rest jedoch schon.
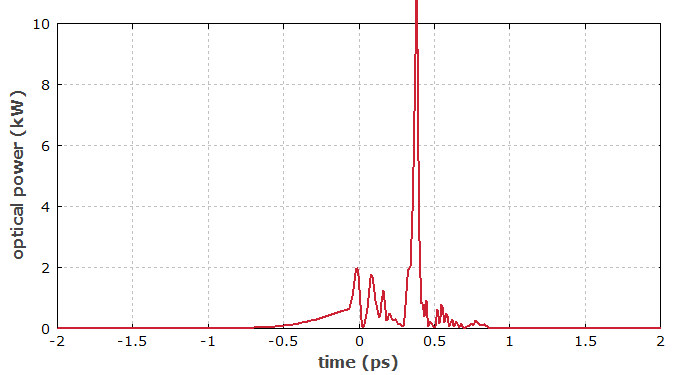
Abbildung 3 zeigt das Spektrum des Pulses auf einer logarithmischen Skala. Eine starke spektrale Verbreiterung ist erkennbar.
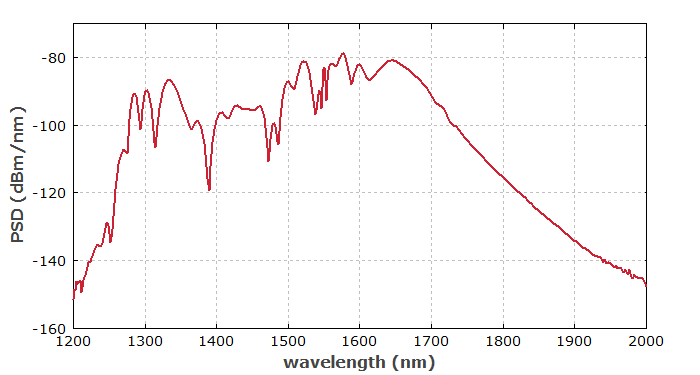
Abbildung 4 zeigt, wie sich das Pulsspektrum in der Faser entwickelt. Die spektrale Verbreiterung beginnt langsam und wird dann stärker, um dann nicht mehr wesentlich weiter zu wachsen.
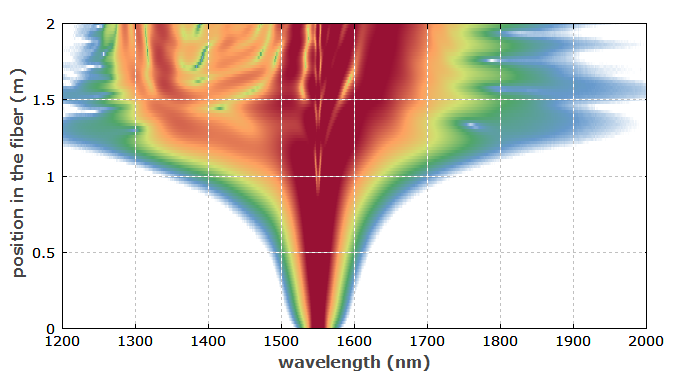
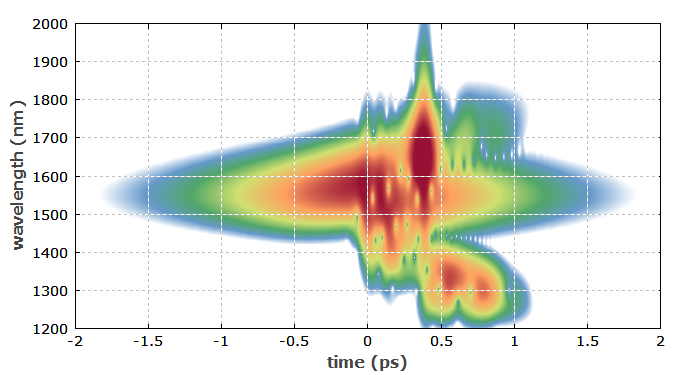
Abbildung 5 ist das Spektrogramm des Pulses am Ende der Faser. Die Farbskala wurde logarithmisch gewählt, so dass auch schwache Ausläufer gut sichtbar sind.