
RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: Pulserzeugung in einem gütegeschalteten Nd:YAG-Laser (mit numerischer Strahlpropagation)
Beschreibung des Modells
Wir simulieren die Pulserzeugung in einem aktiv gütegeschalteten Nd:YAG-Laser ähnlich wie in einem anderen Demo-Fall. Diesmal legen wir jedoch nicht die Annahme zugrunde, dass der Strahlradius immer in etwa durch den Radius der Grundmode des Resonators bestimmt ist. Stattdessen nehmen wir eine volle numerische Strahlpropagation (Wellenpropagation) vor, so dass wir diesen Aspekt überprüfen können. Das ist vorteilhaft, da wir nicht sicher wissen können, wie stark sich gain guiding auswirken wird. Schließlich wird die Laserverstärkung beim Güteschalten oft ziemlich hoch.
Das Modell wird wie folgt aufgestellt:
- Wir definieren ein “beam propagation device”, welches sowohl den 10 mm langen Nd:YAG-Kristall als auch einen Luftspalt von 20 mm Länge enthält. Der Brechungsindex und die Nd-Konzentration werden über Funktionen definiert, die je nach z-Koordinate den richtigen Wert innerhalb oder außerhalb des Kristalls angeben. (Wir könnten leicht auch eine thermische Linse einbauen.)
- Eine feste Intensitätsverteilung der Pumpwelle wird definiert mit transversalem Gauß-Profil (100 μm Radius). Die z-Abhängigkeit bestimmen wir über die Grundzustandsabsorption (unter Vernachlässigung von Sättigung der Pumpabsorption). Da wir beliebige Funktionen verwenden können, kann man einfach auch z. B. eine horizontale Fehljustage des Pumpstrahls einbauen.
- Die fokussierende Wirkung des rechten Resonatorendspiegels und die Verluste am Auskoppelspiegel links werden durch Amplitudenfaktoren beschrieben, die in das “beam propagation device” links und rechts eingebaut werden. (Man könnte solche Faktoren überall einbauen.) Der Einfachheit halber lassen wir den Q-switch im Modell weg; während der Pulsbildung hat er ja keine wesentliche Funktion.
- Wir simulieren dann das Pumpen mit 1500 mW über 250 μs. Dies erzeugt eine erhebliche Verstärkung im Kristall.
- Für die Pulsbildung starten wir mit einem Gauß-Strahl mit 100 W. (Dies ist weit weniger als die erwartete Spitzenleistung.) Wir simulieren dann 30 Umläufe im Resonator, was nur wenige Sekunden dauert. Nach jedem Umlauf plotten wir die Leistung und den momentanen Strahlradius und speichern das Strahlprofil für spätere Verwendung. Ebenfalls integrieren wir die Strahlprofile, um die gesamte Fluenz des Pulses zu erhalten.
Ergebnisse
Abbildung 1 zeigt, wie sich die Leistung und der Strahlradius während des Pulses entwickeln. Der Strahlradius, berechnet über das zweite Moment des Intensitätsprofils, bleibt relativ nahe beim berechneten Wert der Grundmode.
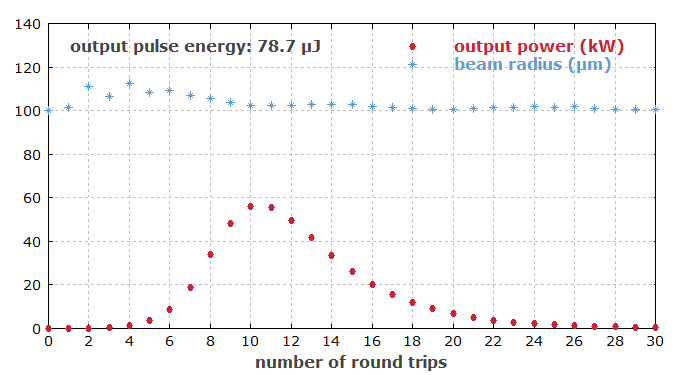
Abbildung 2 zeigt das Nd-Anregungsprofil nach dem Puls. Man erkennt, dass die äußere Region nicht ganz abgeräumt wird, obwohl der Pumpstrahl den gleichen Radius hatte wie die Lasermode.
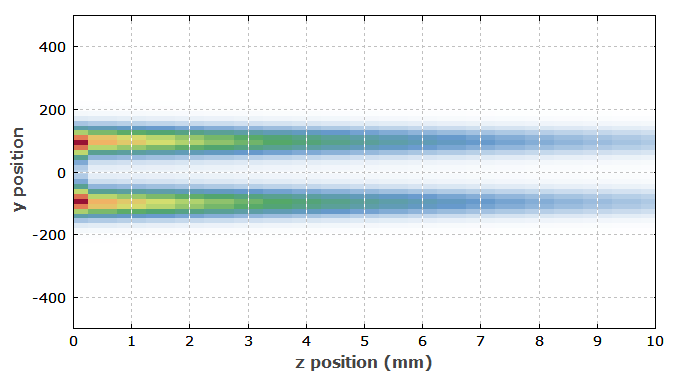
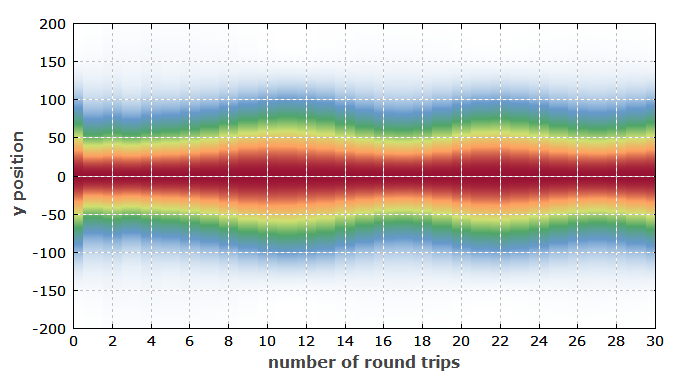
Abbildung 3 zeigt die Entwicklung des Strahlprofils während des Pulses. Es gibt eine deutliche Variation des Profils, verursacht durch das “gain guiding” als Folge des gaußförmigen Pumpprofils. Jedoch sollte dies normalerweise keinen allzu starken Effekt auf den Laser oder auf eine Anwendung haben.
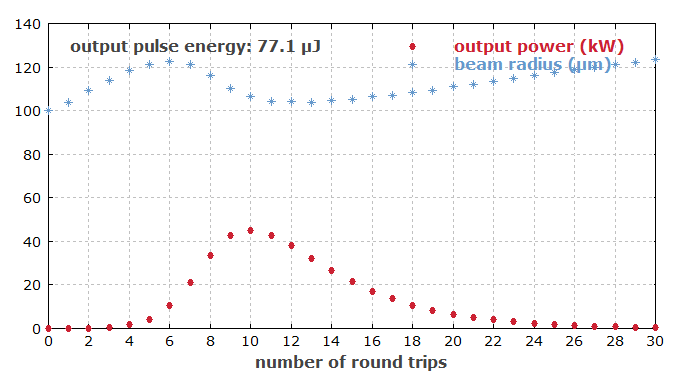
Wenn die Größe der Lücke zwischen Kristall und Endspiegel zwischen 20 mm und 30 mm variiert wird, bleibt der Strahlradius der Resonatormode am linken Ende sehr nahe bei 100 μm. Deswegen überrascht es nicht, dass man für einen Abstand von 30 mm annähernd die gleichen Resultate (hier nicht gezeigt) wie für 20 mm (wie oben) erhält. Sicher würde man dann auch für 25 mm nichts anderes erwarten. Wenn wir das probieren, geschieht aber doch etwas sehr Unerwartetes. Der Strahlradius variiert nun stark, und die Pulsenergie sinkt deutlich ab:
Betrachten Sie außerdem wieder die Entwicklung des Strahlprofils:
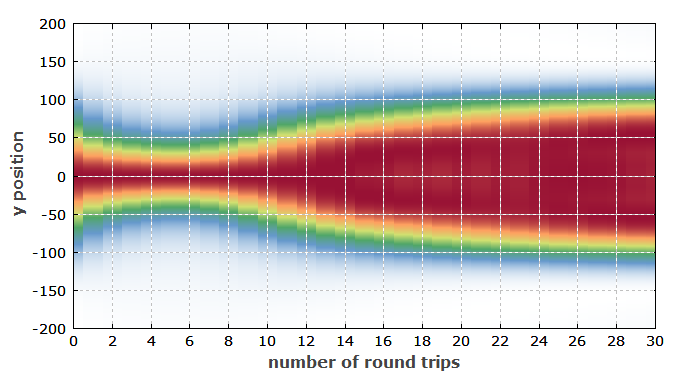
Man sieht, dass sich der Strahl während des Pulsaufbaus stark einschnürt, um später dann wieder stark zu expandieren. (Trotz der ursprünglichen Einschnürung steigt hier der Strahlradius aus dem zweiten Moment wegen stärkerer Ausläufer des Profils.) Im zeitlich integrierten Profil (hier nicht gezeigt) erkennt man nicht viel – nur eine gewisse Abweichung von der Gauß-Form. Für etwas andere Parameter kann man auch eine ausgeprägte Ringform am hinteren Ende des Pulses erhalten, die man freilich nur mit zeitaufgelösten Messungen experimentell nachweisen könnte.
Offenbar reagiert der Resonator in diesem Fall viel sensibler auf das gain guiding als zuvor – aber warum? Der Grund ist gewiss nicht offensichtlich. Eine Analyse des Resonatordesigns (durchgeführt mit der Software RP Resonator) zeigt, dass gerade für 25 mm Abstand die Gouy-Phasenverschiebung des Resonators pro Umlauf 1,59 rad wird, was nahe an π / 2 (≈ 1,57 rad) liegt. Das führt dazu, dass die TEM40- und die TEM22-Moden Resonanzfrequenzen haben, die mit solchen von Grundmoden zusammenfallen. Dadurch kann eine resonante Modenkopplung erfolgen, die starke Änderungen des Strahlprofils verursacht (siehe R. Paschotta, “Beam quality deterioration of lasers caused by intracavity beam distortions”, Opt. Express 14 (13), 6069 (2006)). Diese Resonanzen sind meist recht schmal; im vorliegenden Fall werden die Effekte viel schwächer, wenn man den Abstand nur wieder um 2 mm ändert (auf 23 mm oder 27 mm).
Einige Erkenntnisse aus dieser Übung:
- Gain guiding kann in solchen Lasern relativ stark sein, wird aber trotzdem meist keinen allzu starken Einfluss haben. Jedoch wird der Laser in einem Fall mit resonanter Modenkopplung sehr sensitiv auf solche Effekte.
- Simulationen der Wellenausbreitung können interessante Features zeigen, die man leicht übersehen würde mit Modellen, denen gewisse Annahmen zugrunde liegen (etwa ein konstanter Strahlradius).
- Mit experimentellen Tests würde man diese Effekte ebenfalls leicht übersehen, da man zeitlich aufgelöste Intensitätsprofile aufnehmen müsste.
Und ein weiteres Mal sehen Sie: Obwohl RP Fiber Power für Faserlaser entwickelt wurde, kann man es wegen seiner hohen Flexibilität auch bestens für Bulk-Laser verwenden.
