RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: parabolische Pulse in einem Faserverstärker
Beschreibung des Modells
Hier simulieren wir numerisch die Verstärkung von ursprünglich ungechirpten ultrakurzen Pulsen in einem Yb-dotierten Faserverstärker mit normaler chromatischer Dispersion.
Der folgende Code definiert die Startpulse, die relevanten Fasereigenschaften und einige numerische Parameter:
lambda0 := 1030 nm
E0 := 0.1 nJ { initial pulse energy }
tau0 := 100 fs { initial pulse duration }
GVD_f := 20000 fs^2 { per meter }
n2_f := 3e-20 { nonlinear index }
N_t := 2^10 { number of grid points }
T := 60 * tau0 { width of temporal range }
DoPulsePropagation() :=
begin
set_pulse_grid(T, N_t, lambda0);
startpulse_G(E0, tau0, 0);
set_n2(n2_f); { nonlinear index }
set_GVD(GVD_f); { group velocity dispersion (no higher-order dispersion) }
pp_fiber(1, signal);
end
Die Zentralwellenlänge und die Modenfläche werden von der Definition des optischen Kanals genommen (hier nicht gezeigt).
Wenn nötig, könnte man Dispersion höherer Ordnung hinzufügen (ggf. mit dem mode solver berechnet), ebenfalls stimulierte Raman-Streuung, kompliziertere Eingangs-Pulsprofile, etc.
Ergebnisse
Abbildung 1 zeigt den resultierenden verstärkten Puls in der zeitlichen Domäne. Wegen der Kerr-Nichtlinearität und der chromatischen Dispersion wird der Puls sehr viel länger als der ursprüngliche Puls und weist einen starken “Up-Chirp” auf. Die Pulsform ist etwa parabolisch. Die Details hängen kaum von den Eigenschaften des Startpulses ab; beispielsweise sind sie recht ähnlich, wenn dessen Dauer verdoppelt wird.
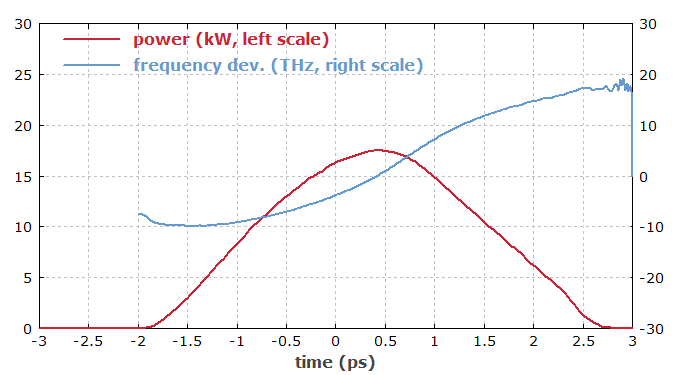
Abbildung 2 zeigt das Spektrum und die spektrale Phase des verstärkten Pulses. Der etwa parabolische Verlauf der spektralen Phase zeigt, dass dispersive Kompression allein mit Dispersion zweiter Ordnung für eine starke Pulskompression gut geeignet sein sollte. (Hierzu mehr weiter unten.)
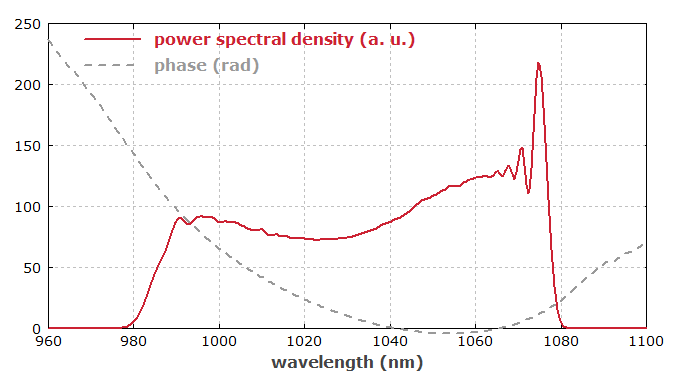
Abbildung 3 zeigt das Spektrogramm des Pulses nach der Faser. Auch hier kann man den Up-Chirp erkennen.
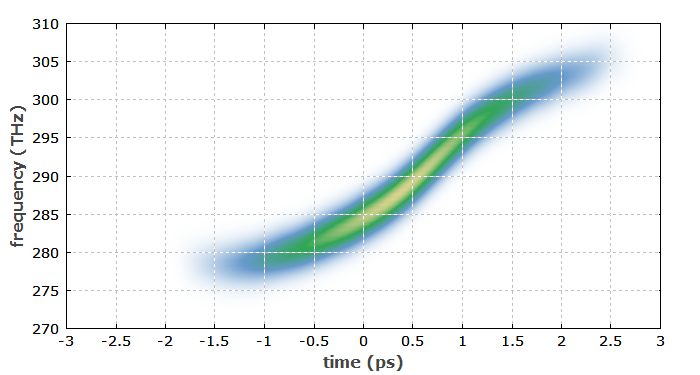
Abbildung 4 zeigt, wie sich die optische Bandbreite, die Energie und die Dauer des Pulses in der Faser entwickeln. Die optische Bandbreite wird auf einem Niveau von 1 % des Spitzenwerts der spektralen Leistungsdichte gemessen.
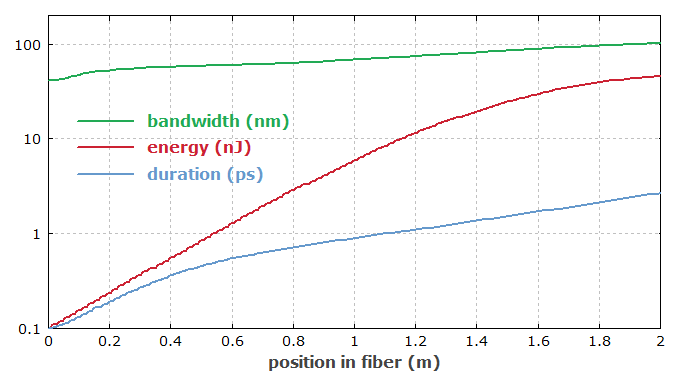
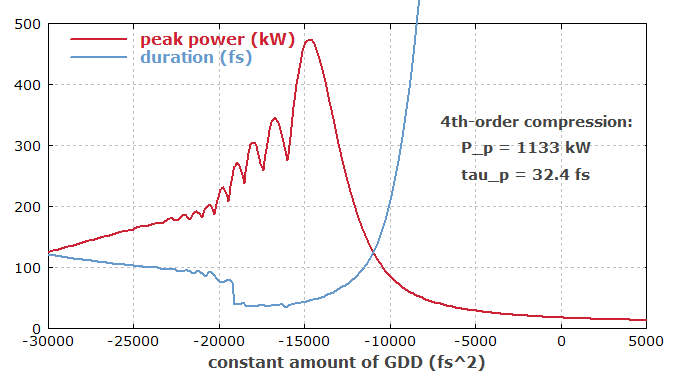
Abbildung 5 zeigt, wie die verstärkten Pulse in einem dispersiven Kompressor zeitlich komprimiert werden könnten. Die Spitzenleistung und die Pulsdauer werden als Funktionen der angewandten Dispersion zweiter Ordnung gezeigt. Die beste Kompression wird für eine Dispersion von ca. −15 000 fs2 erzielt. Ebenfalls wird in Textform angezeigt, welche Kompressions-Resultate man erzielen würde mit einem Kompressor, dessen Dispersion bis zur vierten Ordnung optimiert wäre.