RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: modengekoppelter Faserlaser
Beschreibung des Modells
Hier simulieren wir numerisch die Pulsbildung in einem modengekoppelten Faserlaser mit überall normaler Dispersion (→ dissipative soliton laser). Verglichen mit einem typischen modengekoppelten Bulk-Laser oder auch einem Soliton-Faserlaser ist der Prozess der Pulsformung hier ziemlich kompliziert. Es gibt ein Zusammenspiel starker nichtlinearer Effekte, spektraler Filterung und sättigbarer Absorption. Die Pulsformung in solchen Lasern wurde diskutiert in W. H. Renninger et al., “Pulse shaping and evolution in normal-dispersion mode-locked fiber lasers”, IEEE J. Sel. Top. Quantum Electron. 18 (1), 389 (2012)
In jedem Resonatorumlauf durchläuft der Puls die folgenden optischen Komponenten:
- einen Auskoppler mit wellenlängen-unabhängiger Transmission (der Einfachheit halber)
- ein spektrales Bandpass-Filter
- eine passive Faser
- eine ytterbium-dotierte Faser
- eine weitere passive Faser
- einen sättigbaren Absorber
Die bedeutet, dass wir für dieses Modell drei verschiedene Fasern definieren müssen.
Ein interessantes Details ist die Behandlung der Gain-Sättigung. Normalerweise würde das System Millionen von Resonatorumläufen brauchen, um den stationären Zustand zu erreichen. Da aber hier die Gain-Dynamik (with langsamen Relaxationsoszillationen) nicht von Interesse ist, wurde eine Lösung gewählt, die uns den stationären Zustand weitaus schneller finden lässt – innerhalb von nur 100 Umläufen. In jedem Umlauf wird die Verstärkung in der aktiven Faser für den stationären Zustand berechnet, der sich (nach vielen Umläufen) für die gegebene Durchschnittsleistung des Signals ergeben würde. Durch die große Flexibilität von RP Fiber Power lassen sich solche Kunstgriffe einfach implementieren.
Ergebnisse
Abbildung 1 zeigt die zeitabhängige optische Leistung in den ersten 100 Resonatorumläufen. Ebenfalls wird die instantane Frequenz gezeigt, an der man den starken Up-Chirp der Pulse erkennt.
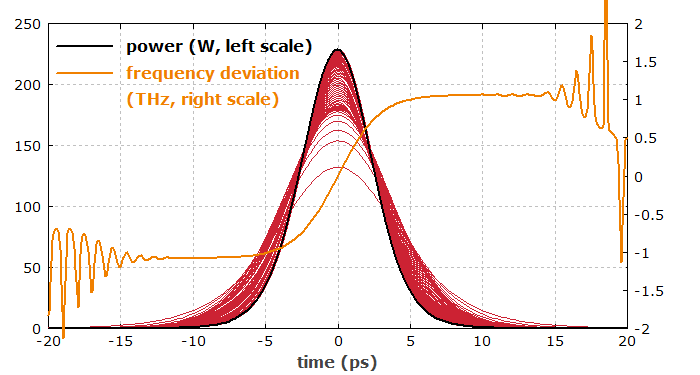
Abbildung 2 zeigt die gleichen Pulse in der Frequenzdomäne. Man erkennt, dass das optische Spektrum eine etwa rechteckige Form erhält, während die spektrale Phase etwa parabolisch wird, zumindest in dem Frequenzbereich mit wesentlicher spektraler Leistungsdichte.
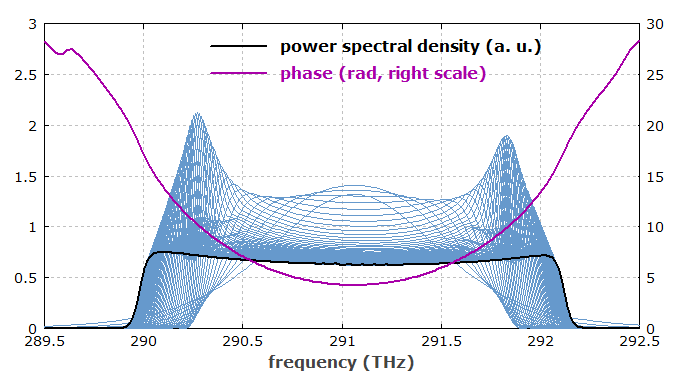
Abbildung 3 zeigt, wie die erzeugten Pulse dispersiv komprimiert werden können. Die Stärke der chromatischen Dispersion für optimale Pulskompression wird automatisch berechnet. Die schwachen Seitenpulse rühren von der etwa rechteckigen Form des Spektrums her, nicht etwa von nicht perfekter Dispersionskompensation.
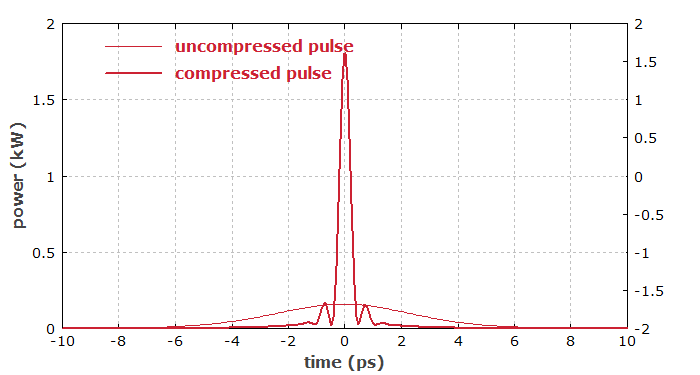
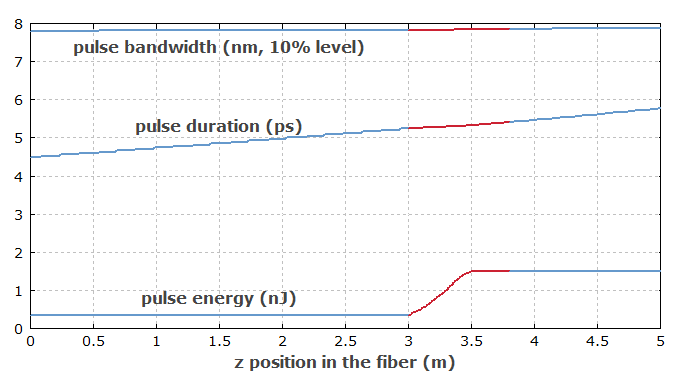
Abbildung 4 zeigt, wie sich die Pulsparameter in den ersten 100 Resonatorumläufen entwickeln. Man sieht, dass das System danach nahe am stationären Zustand ist.
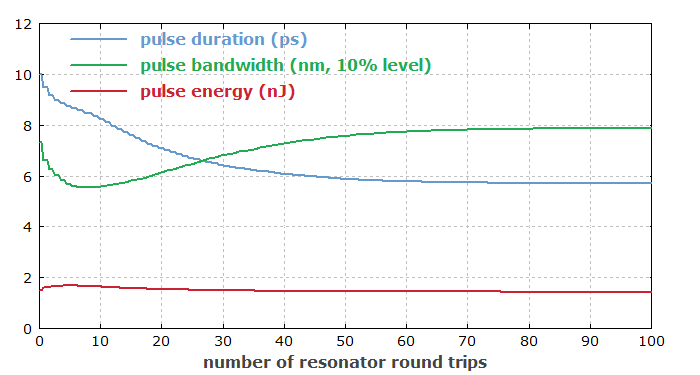
Abbildung 5 zeigt die Pulsparameter in den drei Fasern. Die Kurven werden in den passiven Faser blau gezeigt, in der aktiven Faser rot.