Software > RP Fiber Power > Demo > FBG-Koppler

RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser

Beispiel: Kopplung von Moden in einem Faser-Bragg-Gitter

Hier zeigen wir, wie die Features für numerische Strahlpropagation in RP Fiber Power genutzt werden können, um die Lichtausbreitung in Faser-Bragg-Gittern zu untersuchen. Dazu muss man ein wenig programmieren, aber Sie werden sehen, dass es eigentlich gar nicht schwer ist.

Beschreibung des Modells

Wir müssen zunächst einmal das Brechungsindexprofil der Faser definieren, von dem das Fasergitter hergestellt wird:

n_cl := 1.44  { cladding index }
n_co := n_cl + 2e-3  { core index }
r_co := 30 um  { core radius }
r_cl := 40 um  { region where n must be exactly constant }
L_f := 200 mm  { length of the simulated region }
 
n_f(r):= { index of pure fiber }
  if r <= r_cl then
    n_cl + exp(-ln(2) * (r / r_co)^8) * (n_co - n_cl)
  else
    n_cl

Anstelle eines einfachen Stufenprofils haben wir hier eine Super-Gauß-Funktion verwendet.

Nun verwenden wir dies für den “mode solver”, um zunächst einmal zu prüfen, wie viele Moden die Faser hat:

calc set_n_profile("n_f", r_cl)
for m := 1 to m_max(lambda) do
  show "LP0" , m, ": ", beta_lm(0, m, lambda) * um:f6:" / µm"

Dann können wir den “mode solver” auch verwenden, um die Differenz der Phasenkonstanten der Grundmode und einer bestimmten höheren Mode zu berechnen. Daraus erhalten wir dann die nötige Periode des Fasergitters für eine effektive Kopplung der Moden:

l_target := 0  { targeted mode }
m_target := 3
dbeta := beta_lm(0, 1, lambda) - beta_lm(l_target, m_target, lambda)
show "dbeta:  ", dbeta * um:f6:" / µm"
p := 2pi / dbeta
show "Period: ", p:d3:"m"

Nun definieren wir das dreidimensionale Brechungsindexprofil des Faser-Bragg-Gitters:

n_FBG(x, y, z):=  { index of fiber Bragg grating }
  begin
    var r;
    r := sqrt(x^2 + y^2);
    if r <= r_cl
    then n_cl
     + exp(-ln(2) * (r / r_co)^8) * (n_co - n_cl) * (1 + 0.1 * sin(dbeta * z))
    else n_cl;
  end

Danach können wir die numerische Strahlpropagation durchführen:

; Grid parameters for numerical beam propagation:
r_max := 4 * r_co
N_r := 2^7
dr := 2 * r_max / N_r
dz := 200 um
N_z := L_f / dz
N_s := 20  { number of sub-steps for each dz interval }
 
calc
  begin
    bp_set_device(1);
    bp_set_grid(r_max, N_r, r_max, N_r, L_f, N_z, N_s);
    bp_define_channel(lambda);
    bp_set_n_z('n_FBG(x, y, z)', 'z');
    bp_set_A0('A_lm_xy(0, 1, lambda, x, y)');  { fundamental mode as the input field }
  end

Schließlich können wir die Funktion bp_I() verwenden, um einfarbiges Diagramm für die Verteilung der optischen Intensität zu erstellen. Zusätzlich können wir ein paar Zeilen Code einsetzen, um die Entwicklung der optischen Leistung in den beiden Moden zu verfolgen:

diagram 1:
 
x: 0, L_f / mm
"z (mm)", @x
y: -r_max / um, +r_max / um
"y (µm)", @y
y2: 0, 100
"optical powers (%)", @y2
frame
hx
hy
 
! I_max := 1.5 * bp_I_max(0)
cp: color_I((bp_I(0, y * um, x * mm) / I_max)),
  order := yx
 
P_lm(l, m, z) := 
  { power in LP_lm mode at position z }
  abs2(int(int(bp_A%(x, y, z) * A_lm_xy(l, m, lambda, x, y),
    x := -r_max to +r_max step dr),
    y := -r_max to +r_max step dr))
 
f: 100 * P_lm(0, m_target, x * mm), yscale = 2,
  color = red, width = 1, ["LP", l_target, m_target, " power"]
 
f: 100 * P_lm(0, 1, x * mm), yscale = 2,
  color = blue, width = 1, "LP01 power"

Wir erhalten damit das folgende Diagramm:

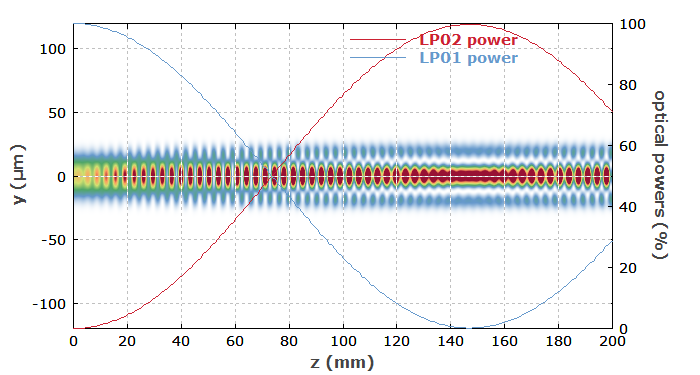
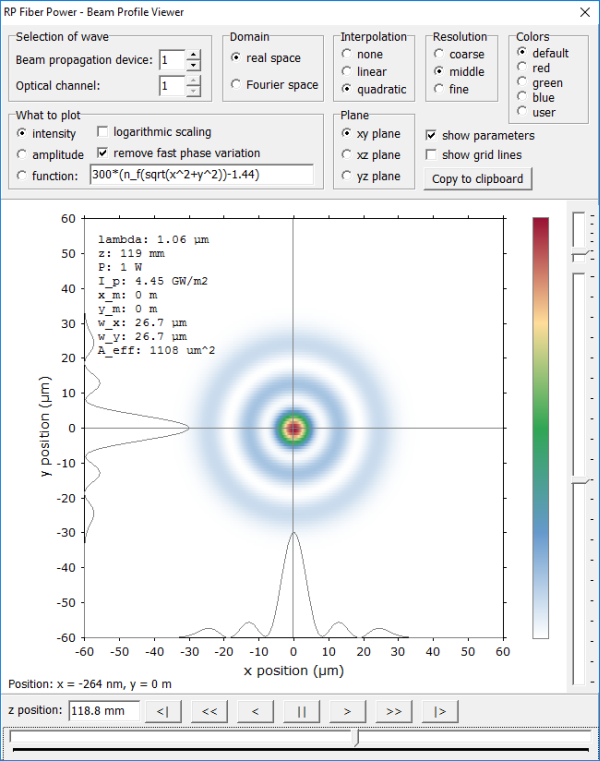
Um die Details des Geschehens interaktiv zu erkunden, können Sie auch ein interaktives Fenster verwenden:

Es ist ebenfalls interessant, die Entwicklung der Leistungen in den Moden am Beginn des Fasergitters zu untersuchen:

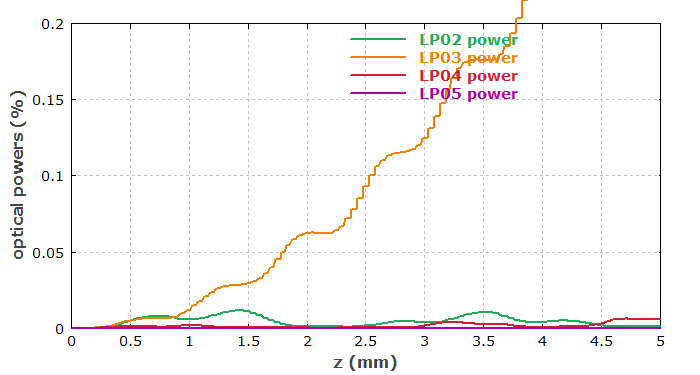
Man sieht, dass nur die Leistung in der LP₀₃-Mode konsistent ansteigt, während die Leistungen der anderen Moden auf niedrigem Niveau oszillieren. Dies liegt daran, dass die Beiträge der Kopplung in diese Moden, die an verschiedenen Stellen entlang des Fasergitters auftreten, im Allgemeinen unterschiedliche Phasenwerte haben – außer für die eine Mode, für die wir dies durch geeignete Wahl der Gitterperiode kompensiert haben.

Natürlich wäre es nicht schwierig, diverse Details des Modells zu verändern oder zusätzliche Diagramme zu erstellen. Beispielsweise könnten Sie die Effekte asymmetrischer Gitter untersuchen, oder von annähernd entarteten Moden in Fasern mit hoher Zahl von Moden, ebenso die Auswirkungen von Biegungen der Faser oder was immer sonst Ihnen in den Sinn kommt!

(zurück zu der Liste der Beispiele)