RP Coating – Advanced Software for
Designing Optical Multilayer Structures

Here, we develop a rugate filter, where the refractive index varies continuously within the structure. This could be fabricated, for example, by mixing SiO₂ and Nb₂O₅ during coating deposition.

For numerical modeling, we describe the structure as being composed of many very thin layers. If sufficiently small steps are chosen, the refractive index steps from one layer to the next one are so small that the results are very accurate.

The filter is supposed to reflect light only for wavelengths around 1000 nm, without exhibiting side lobes as would be obtained for an ordinary Bragg mirror. We can achieve that with a sinusoidal oscillation of the refractive index, when we also observe two other issues:

• We need to avoid additional reflections from refractive index steps at both ends, e.g. by having smooth transitions there.
• We also need to apodize the structure, i.e., to decrease the oscillation amplitude towards the ends.

Overall, this leads to a somewhat complicated structure, which we certainly would not like to define by entering hundreds of precalculated refractive index values. Instead, we want to describe the whole structure with a couple of parameters, and have everything calculated from these.

We first define only the substrate and the superstrate – for now assuming that both are made of BK7 glass:

beam from superstrate
substrate: BK7
; no layers defined yet
superstrate: BK7

(We will replace the superstrate with air later on.)

We assume that we can realize only index values above that of BK7. Therefore, we define an elevated refractive index n0 around which we can later have the oscillation. Around the reflecting region with the oscillation, we place two matching regions where the refractive index smoothly varies from that of BK7 to n0 and later back again:

l_ref := 1000  { reference wavelength }
 
n_s := n(-1, l_ref)  { substrate index }
n0 := n_s + 0.3  { medium index in reflecting region }
 
n_rug(l, x) := n_BK7(l) + x  { rugate material, e.g. realized as SiO2 mixed with Nb2O5 }
 
; Parameters of the index matching regions:
z_m := 1000  { thickness }
dz_m := 20  { resolution }
x_m(z) := (n0 - n_s) * (10 * z^3 - 15 * z^4 + 6 * z^5)
 
; Parameters of the reflecting region:
z_r := 10000  { approximate thickness }
dz_r := 25  { resolution }
Lambda := l_ref / (2 * n0)  { oscillation period }
z_r := Lambda * round(z_r / Lambda)  { thickness correction }
W(x) := exp(-15 * (x - 0.5)^2)  { window function }
si(x) := if sin(x) >= 0 then 1 else -1
x_r(z) := (n0 - n_s) * (1 + sin(2pi * z / Lambda) * W(z / z_r))
 
MakeStructure() := 
  { Make the coating structure based on the parameters above }
  begin
    while nolayers() > 0 do remove_layer(1);
      { allow repeated application: remove all already existing layers }
    { index matching region }
    for z := 0 to z_m step dz_m do
      add_layer(nolayers() + 1, "rug", x_m(z / z_m), dz_m, 0, 0);
    { reflecting part }
    for z := 0 to z_r step dz_r do
      add_layer(nolayers() + 1, "rug", x_r(z), dz_r, 0, 0);
    { index matching region }
    for z := 0 to z_m step dz_m do
      add_layer(nolayers() + 1, "rug", x_m(1 - z / z_m), dz_m, 0, 0);
  end
 
calc MakeStructure()
 
show "Thickness: ", get_d(0) * d_units:d3:"m"

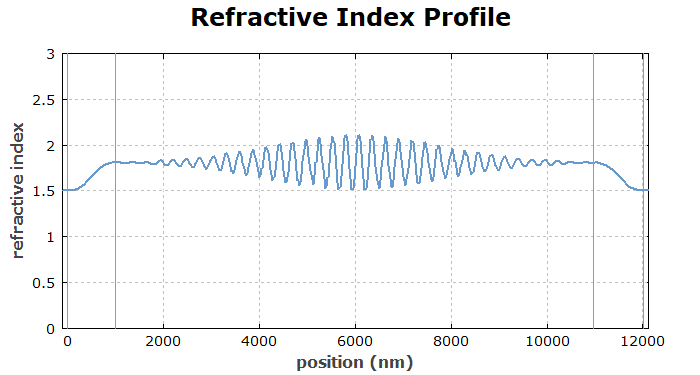
Then we first want to see how the created index profile looks:

diagram 1:
 
"Refractive Index Profile"
 
x: -100, get_d(0) + 100
"position (nm)", @x
y: 0, 3
"refractive index", @y
frame
hx
hy
 
f: n(x,1000), color = blue, step = 1
 
! begin
    setcolor(gray);
    line(0,i * CS_y2);
    line(z := z_m,z + i * CS_y2);
    line(z := z_m + z_r,z + i * CS_y2);
    line(z := get_d(0),z + i * CS_y2);
  end

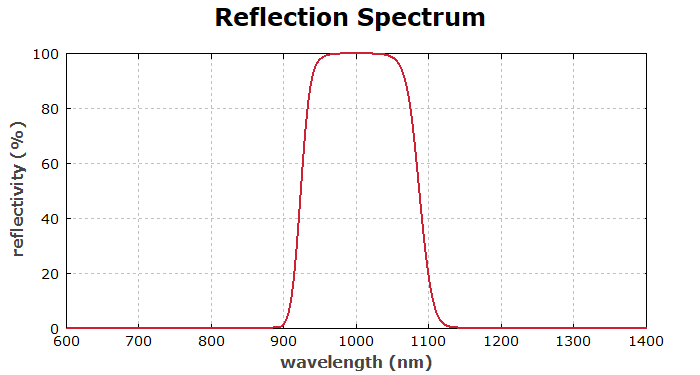
Then we want to see the obtained reflectivity spectrum:

diagram 2:
 
"Reflection Spectrum"
 
x: 600, 1400
"wavelength (nm)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
 
f: 100 * R(x), color = red, step = 1, maxconnect = 1

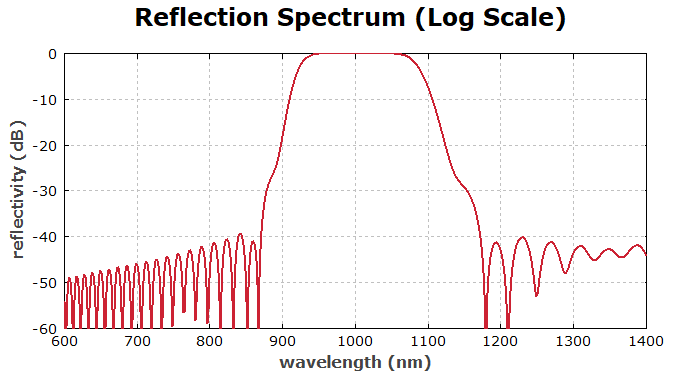
Indeed this works quite well. We can inspect the side lobes more closely with a logarithmic scale:

diagram 3:
 
"Reflection Spectrum"
 
x: 600, 1400
"wavelength (nm)", @x
y: -60, 0
"reflectivity (dB)", @y
frame
hx
hy
 
f: 10 * lg(R(x)), color = red, step = 1, maxconnect = 1

Next we want to modify the structure such that it works against air as the superstrate. If we only change the superstrate to air, we have a Fresnel reflection at the surface and therefore obtain a decreased performance of the filter:

diagram 4:
 
"Reflection Spectrum Against Air"
 
x: 600, 1400
"wavelength (nm)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
 
! set_layer(nolayers() + 1, "air", 0, 0, 0, 0)
 
f: 100 * R(x), color = red, step = 1, maxconnect = 1

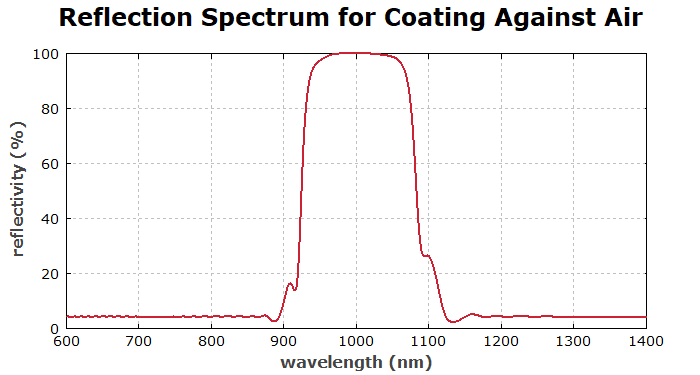
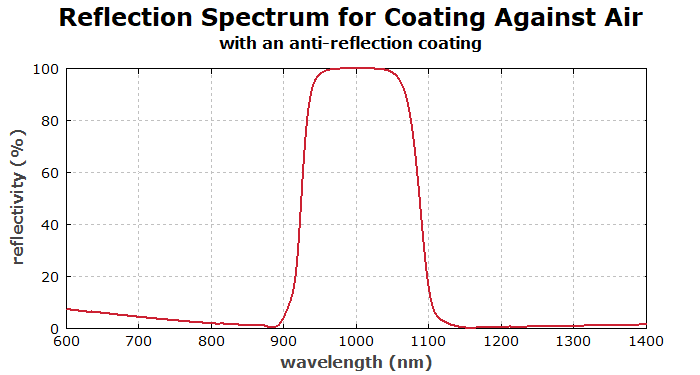
We can improve the performance by first removing the index-matching region and then using an anti-reflection structure. As the simplest possibility, we use a single-layer AR coating:

diagram 5:
 
"Reflection Spectrum Against Air"
 
"with an anti-reflection coating"
 
x: 600, 1400
"wavelength (nm)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
 
! for z := 0 to z_m step dz_m do remove_layer(nolayers())
  { remove the top index-matching region }
 
! begin  { add a single-layer AR coating }
    n_ar := sqrt(n0);  { refractive index of anti-reflection layer }
    x_ar := n_ar - n_fsilica(l_ref * l_units);  { corresponding x value }
    add_layer(nolayers() + 1, "rug", x_ar, l_ref / 4 / n_ar, 0, 0);
  end
 
f: 100 * R(x), color = red, step = 1, maxconnect = 1

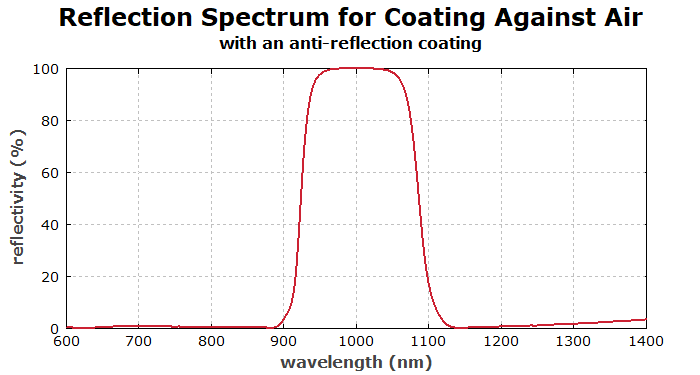
For improved performance, we use a multilayer AR structure, numerically optimized elsewhere:

! begin  { add previously calcultaed AR coating, optimized for n0 = 1.8075 }
    add_layer(nolayers() + 1, "TiO2", 0, 34.6, 0, 0);
    add_layer(nolayers() + 1, "SiO2", 0, 23.7, 0, 0);
    add_layer(nolayers() + 1, "TiO2", 0, 127.8, 0, 0);
    add_layer(nolayers() + 1, "SiO2", 0, 20.8, 0, 0);
    add_layer(nolayers() + 1, "TiO2", 0, 42.6, 0, 0);
    add_layer(nolayers() + 1, "SiO2", 0, 151.9, 0, 0);
  end

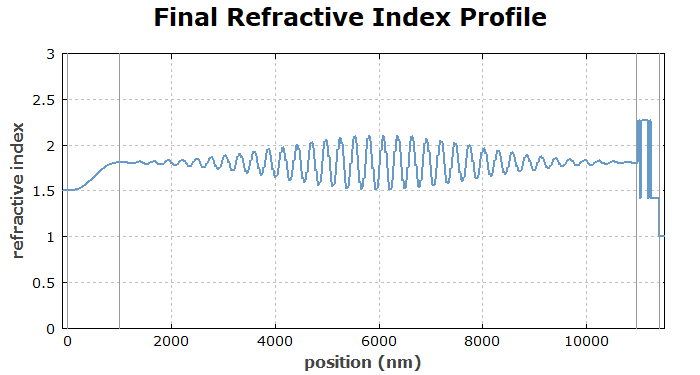
The finally obtained index profile is as follows:

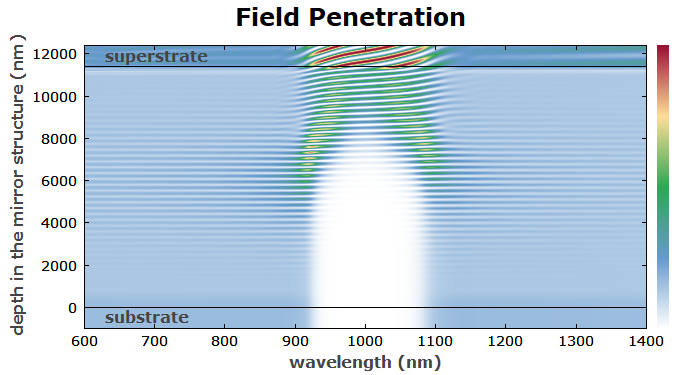
Finally, we show the field penetration: