RP Coating – das Software-Werkzeug für das Design optischer Vielschichtstrukturen

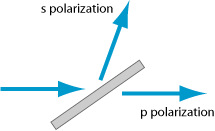
Wir entwerfen hier das Design für einen Dünnschichtpolarisator, der eine Beschichtung nur auf einer Seite eines Substrats benötigt. Der Einfallswinkel wird als der Brewster-Winkel gewählt, so dass die Reflexion an der Rückseite für p-Polarisation entfällt. Wir benötigen also eine Beschichtung, die bei der Design-Wellenlänge von 1064 nm für s-Polarisation hoch reflektierend und für p-Polarisation gut durchlässig ist.

Im Formular kann man die Materialien festlegen, einige Designparameter bestimmen und die grafischen Diagramme auswählen:

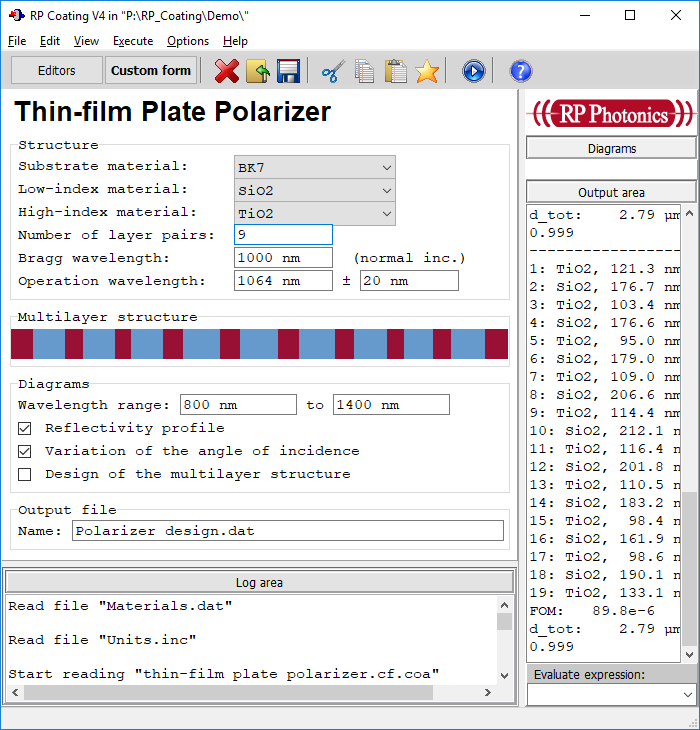
Das Formular und die Berechnungen sind nicht fest kodiert, sondern in Form eines Skripts implementiert. Im Folgenden zeigen wir einige Details davon.

Die grundlegende Idee für die Struktur ist, so etwas wie einen Bragg-Spiegel zu verwenden, wobei die Design-Wellenlänge innerhalb des Reflexionsbands für s-Polarisation liegt, jedoch gerade außerhalb dieses Bands für p-Polarisation. Ein Bragg-Spiegel ist jedoch nicht sehr geeignet, da er außerhalb des Haupt-Reflexionsbands noch erhebliche Peaks der Reflektivität aufweist. Viel besser ist es, ein Kantenfilter-Design zu verwenden, welches eine modifizierte Version eines Bragg-Spiegels ist: Die beiden äußeren höher brechenden Schichten haben eine Schichtdicke von nur λ / 8 anstelle von λ / 4:

l := 1064  { operation wavelength }
theta := arctan(n_BK7(l * l_units))
N_Bragg := 10  { no layer pairs }
l_B := 1020  { Bragg wavelength for normal incidence }
 
beam from superstrate
substrate: BK7
* TiO2, l / 8 at l_B
for j := 1 to N_Bragg - 1 do
begin
* SiO2, l / 4 at l_B
* TiO2, l / 4 at l_B
end
* SiO2, l / 4 at l_B
* TiO2, l / 8 at l_B
superstrate: air

Wir definieren dann die Zielfunktion:

FOM() := sum(l := 1060 to 1070 step 2, R_p(l,theta)^2 + T_s(l,theta)^2)

Wie immer ist diese so gemacht, dass sie für ein ideales Design 0 ergeben würde, für alle Abweichungen davon jedoch positive “Strafpunkte” vergibt.

Um die Performance noch weiter zu erhöhen, können wir eine einfache lokale Optimierung anwenden:

optimize coating for minimum of FOM()

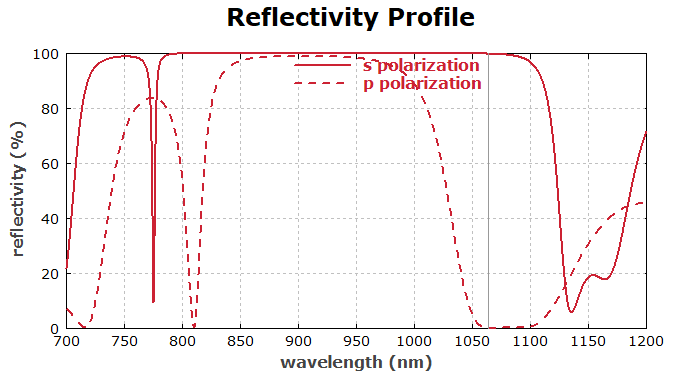
Das erste Diagramm zeigt dann das Reflektivitätsprofil:

diagram 1:
 
"Reflectivity Profile"
 
x: 700, 1200
"wavelength (nm)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
legpos 420, 150
 
f: 100 * R_p(x, theta), "p polarization",
  color = red, width = 3, step = 1
 
f: 100 * R_s(x, theta), "s polarization", style = dashed,
  color = red, width = 3, step = 1
 
! begin  { indicate the design wavelength }
    setcolor(gray);
    line(l, l + i * CS_y2)
  end

Dann testen wie die Empfindlichkeit auf Änderungen des Einfallswinkels:

diagram 2:
 
"Variation of the Angle of Incidence"
 
x: 50, 60
"angle of incidence (°)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
 
f: 100 * R_s(l, x * deg), "s polarization",
  color = red, width = 3
f: 100 * R_p(l, x * deg), "p polarization",
  color = red, width = 3, style = dashed
 
! begin
    setcolor(gray);
    line(theta / deg,theta / deg + i * CS_y2);
  end

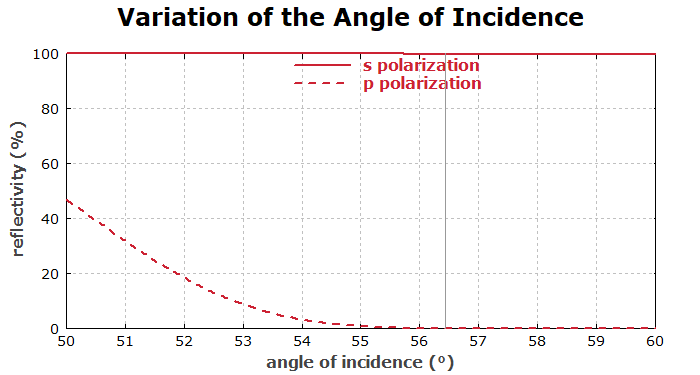
Wir sehen, dass die Reflektivität für p-Polarisation für zu kleine Winkel ansteigen würde, wo allerdings ohnehin auch die Reflektivität der Rückseite ansteigen würde.

Schließlich zeigen wir das erhaltene Design an:

diagram 3:
 
x: -500, get_d(0) + 500
"position (nm)", @x
y: 0, 3
"refractive index (nm)", @y
frame
 
! begin
    for j := 1 to nolayers() do
    begin
      var g;
      g := if get_material$(j) = "TiO2" then 0.8 else 0.9;
      setcolor(rgb(g, g, g));
      box(get_z(j), get_z(j + 1) + i * CS_y2);
    end;
    draw_cs(); { draw the coordinate system again }
  end
 
[get_d(j):f0:"nm"], (get_z(j) + 0.5 * get_d(j))l, (0.03 * CS_y2)c,
  direction = 90, for j := 1 to nolayers()
"substrate", (-200)l, (0.03 * CS_y2)c, direction = 90
"superstrate", (get_d(0) + 200)l, (0.03 * CS_y2)c, direction = 90
 
f: n(x,l), step = 1, color = blue