Software > RP Resonator > Demos > Achromatic lens

RP Resonator – Advanced Software for Laser Resonator Design and Optimization

Example Case: Achromatic Lens

We optimize an achromatic lens doublet for a given focal length over some wavelength range. We assume that BK7 crown glass and SF2 flint glass is used. The basic idea behind such designs is to realize an overall focusing lens by combining a strongly focusing and a less strongly defocusing lens, where the latter exhibits stronger chromatic dispersion. Although the defocusing effect of the second lens is weaker than the focusing effect on the first one, its chromatic aberrations can compensate those of the other lens.

In RP Resonator, we first define the doublet lens as a sequence of two “prisms” with curved interfaces, plus some air space for propagation through air, where we can find the focal point:

resonator: single pass, z = 0, w = w0, d_t = 10 um
* prism (lens1): l = d1, n(l) = n_BK7(l), R1 = R1, R2 = R2
* prism (lens2): l = d2, n(l) = n_SF2(l), R1 = -R2, R2 = R3
* air: d = b, "b"
resonator end

We define a function for locating the focal point and calculating the focal length, based on geometrical ray propagation:

z0 := 0.5 * (d1 + d2) { reference position for focal length }
f_lens(l) :=
  { focal length for wavelength l }
  begin
    global allow all;
    var z, z_f;
    z := f_wanted / 2;
    z_f := z - d_t(z, l) / da_t(z, l);
    z_f - z0;
  end

For the numerical optimization, we first define a figure of merit which “punishes” deviations from the wanted focal length in the relevant wavelength range:

FOM() :=
  { figure of merit: 0 in ideal case }
  sum(l := 400 nm to 800 nm step 50 nm,
    (f_lens(l) / f_wanted - 1)^2)

Then we let the script adjust the curvature radii R2 and R3 such that the figure-of-merit function becomes as small as possible, and display the obtained values:

vary
  R2 in [10 mm, 200 mm],
  R3 in [10 mm, 200 mm],
  for minimum of (Init(0); FOM()),
  ytol = 1e-6
 
show "R1:      ", R1:d3:"m"
show "R2:      ", R2:d3:"m"
show "R3:      ", R3:d3:"m"

Finally, the success is monitored with two diagrams, showing the beam radius versus position for different wavelengths, and the focal length versus wavelength:

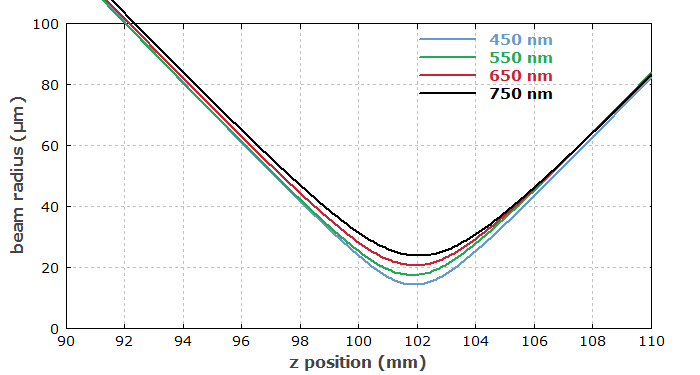
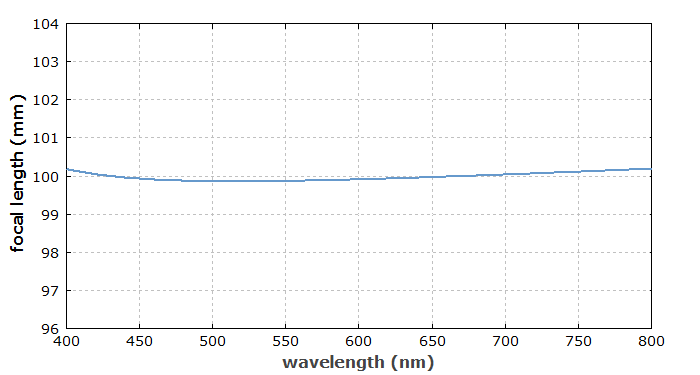
You can see that the software is very flexible concerning the definition of compound optical elements and merit functions, for example. It would be easy to extend that for lens triplets in order to realize apochromat lenses with further improved properties over a wide wavelength range.

(back to the list of example cases)