RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser

Überblick	Features	Geschwindigkeit	Modell
Faser-Daten	Benutzung	Demos	Versionen

Beispiel: Nichtlineare Selbstfokussierung in einer Faser

Beschreibung des Modells

Hier berechnen wir, wie die Grundmode einer Faser schrumpft in Folge des Effekts der nichtlinearen Selbstfokussierung.

Der mode solver berücksichtigt an sich keine nichtlinearen Effekte. Jedoch können wir mit Hilfe einiger Skriptzeilen das Brechungsindexprofil mit seiner nichtlinearen Veränderung abspeichern und daraus die Moden neu berechnen. Dieser Vorgang muss wiederholt werden, bis wir eine selbstkonsistente Lösung erhalten:

dr := 0.05 um
defarray I[0, 200 um, dr]
n_f_nl(r) := n_f(r) + n2 * (if r <= r_max then I~[r])
  { nonlinear refractive index profile }
store_I(P) := 
  for r := 0 to 2 * r_co step dr do
    I[r] := P * I_lm(0, 1, lambda, r)
    { ignore index changes outside 2 * r_co, where the intensity is small }
 
CalcNonlinearMode(P) := 
  { Calculate the lowest-order mode with self-focusing for the power P. }
  begin
    var A, A_l;
    A := 0;
    repeat
      A_l := A;
      store_I(P);
      set_n_profile("n_f_nl", r_max);
      A := A_eff_lm(0, 1, lambda);
    until abs(A_l / A - 1) < 1e-6;
  end

Wir können auch numerisch die Strahlpropagation simulieren und dabei die Nichtlinearität berücksichtigen. Hierfür definieren wir ein numerisches Gitter und setzen diverse Inputs:

x_max := 30 um { maximum x or y value }
N := 2^5 { number of grid points in x and y direction }
dx := 2 * x_max / N { transverse resolution }
z_max := 30 mm { fiber length }
dz := 100 um { longitudinal resolution }
N_z := z_max / dz { number of z steps }
N_s := 100 { number of sub-steps per dz step }
 
P_11 := 4 MW
A0%(x, y) := sqrt(P_11) * A_lm_xy(1, 1, lambda, x, y)  { initial field }
 
calc
  begin
    bp_set_grid(x_max, N, x_max, N, z_max, N_z, N_s);
    bp_define_channel(lambda);
    bp_set_n('n_f(sqrt(x^2 + y^2))'); { index profile }
    bp_set_loss('10e2 * ((x^2 + y^2) / (20 um)^2)^3');  { simulate loss for cladding modes }
    bp_set_n2('n2');
    bp_set_A0('A0%(x, y)'); { initial amplitude }
    bp_set_interpol(2); { quadratic interpolation }
  end

Ergebnisse

Abbildung 1 zeigt das Modenprofil für eine optische Leistung von 5 MW (nicht weit unterhalb der Schwelle für katastrophale Selbstfokussierung) sowie das zugehörige Indexprofil.

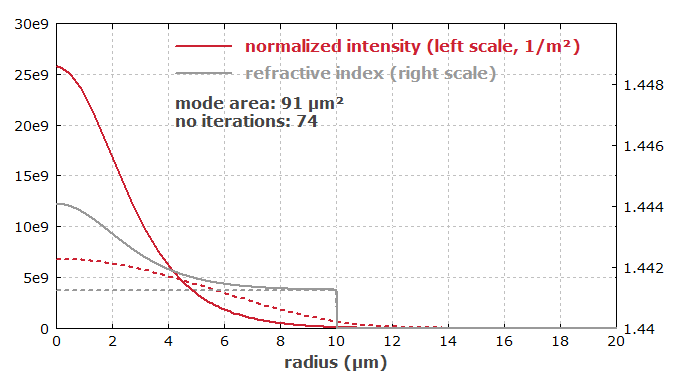
Abbildung 1: Berechnete Intensitätsprofile der Mode mit und ohne Selbstfokussierung. Die Brechungsindizes werden ebenfalls gezeigt. Man erkennt, dass das Indexprofil durch den nichtlinearen Effekt sehr wesentlich verändert wird.

Abbildung 2 zeigt die Modenfläche als Funktion der optischen Leistung. Die Modenfläche nimmt in der Nähe der kritischen Leistung dramatisch ab.

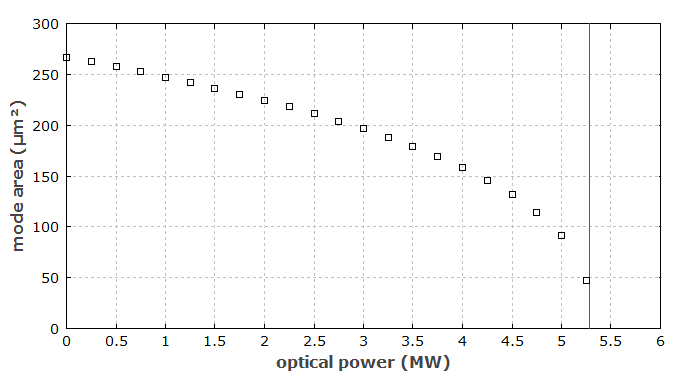
mode area vs. optical power — Abbildung 2: Modenfläche als Funktion der optischen Leistung. Die rote Linie zeigt die kritische Leistung für katastrophale Selbstfokussierung.

Abbildung 3 zeigt die maximale optische Leistung in Abhängigkeit vom Kernradius. Für jeden Radius muss die optische Leistung ermittelt werden, für die die Intensität auf der Faserachse die Zerstörschwelle erreicht. Natürlich muss die Mode für jede Leistung neu berechnet werden.

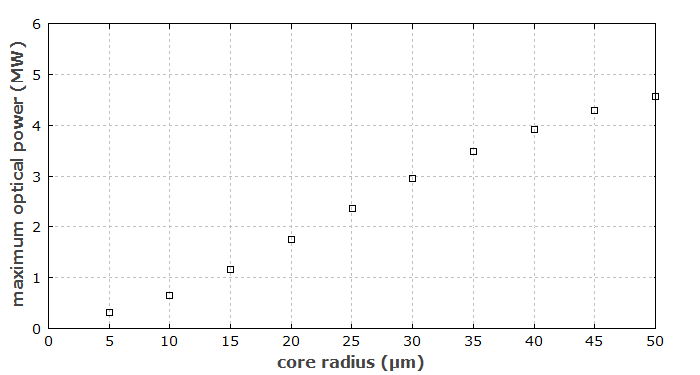
maximum power in fiber vs. core radius — Abbildung 3: Maximale optische Leistung in Abhängigkeit vom Kernradius.

Anfangs nimmt die maximale Leistung proportional zur Kernfläche zu. Für große Faserkerne wird der Anstieg jedoch viel langsamer, da die Modenfläche durch die Selbstfokussierung reduziert wird.

Nun untersuchen wir, was passiert, wenn wir Licht in die LP₁₁-Mode (die erste Mode höherer Ordnung) injizieren, wie sie ohne die Nichtlinearität berechnet wurde. Hierfür benutzen wir eine numerische Simulation der Lichtausbreitung. Abbildung 4 zeigt das Resultat für eine optische Leistung von 4 MW, nicht weit unterhalb der kritischen Leistung für die Selbstfokussierung. Hier wird die LP₁₁-Mode instabil. Schon die kleinste Asymmetrie, hier hervorgerufen durch kleine numerische Fehler, lässt diese Mode nach ca. 10 mm zerfallen in eine Überlagerung der LP₀₁- und LP₁₁-Mode:

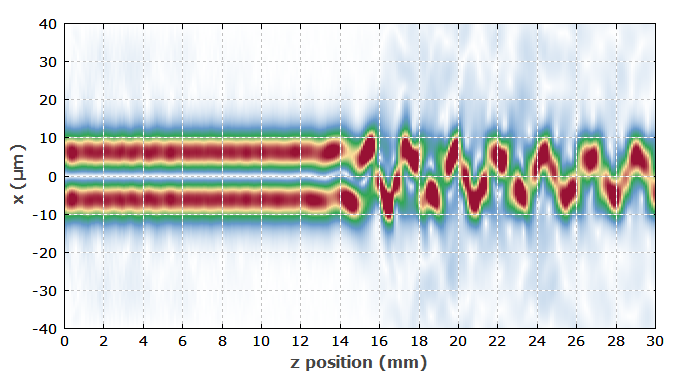
numerical beam propagation with Kerr nonlinearity — Abbildung 4: Amplitudenprofil in der x-z-Ebene, wenn intensives Licht in die LP₁₁-Mode (berechnet ohne Nichtlinearität) geschickt wird.

Wir können ebenfalls die Entwicklung der optischen Leistungen in den Moden verfolgen:

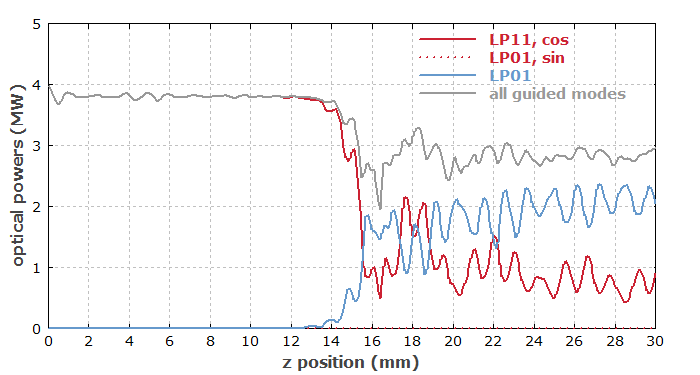
Es mag überraschend erscheinen, dass die gesamte Leistung gewisse Oszillationen zeigt: Wie kann die Leistung an einem Ort wieder steigen, obwohl wir nur Verluste (für die Cladding-Moden) haben? Man kann dies verstehen als einen Energieaustausch mit Cladding-Moden, der durch die Nichtlinearität der Faser ermöglicht wird. Man beachte auch, dass die nichtlineare Wechselwirkung Licht in die Cladding-Moden auskoppelt, was bei niedrigen Leistungen nicht geschehen würde.

(zurück zu der Liste der Beispiele)

RP Fiber Power: Simulations- und Design-Software für Faseroptik, Faserverstärker und Faserlaser

Beispiel: Nichtlineare Selbstfokussierung in einer Faser

Beschreibung des Modells

Ergebnisse

RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser