RP Fiber Power: Simulations- und Design-Software
für Faseroptik, Faserverstärker und Faserlaser
| Überblick | Features | Geschwindigkeit | Modell |
| Faser-Daten | Benutzung | Demos | Versionen |
Beispiel: Biegeverluste einer Faser mit hoher Modenfläche
Hier zeigen wir, wie RP Fiber Power für die Analyse der Effekte der Biegung von Glasfasern verwendet werden kann.
Beschreibung des Modells
Wir betrachten eine Faser mit einfachem Stufen-Index-Profil: Der Kernradius ist 20 μm und die numerische Aperture 0,05. Bei einer Wellenlänge von 1 μm hat diese Faser mehrere geführte Moden, aber man kann trotzdem versuchen, sie nur mit der Grundmode zu betreiben.
Für die Strahlpropagation verwenden wir ein relativ großes numerisches Gitter und simulieren Verluste für die Cladding-Moden mit einer künstlichen Absorption, die mit zunehmender Entfernung vom Faserkern rasch zunimmt.
Der Skript-Code für die Vorbereitung der Strahlpropagation wird hier gezeigt:
; Grid parameters for beam propagation:
r_max := 100 um
N := 2^7
dr := 2 * r_max / N
z_max := 200 mm
dz := 100 um
N_z := z_max / dz
N_s := 5
loss(x, y) := 1e2 * ((x^2 + y^2) / (40 um)^2)^4
calc { set up the beam propagation }
begin
bp_set_grid(r_max, N, r_max, N, z_max, N_z, N_s);
bp_define_channel(lambda);
bp_set_n('n_f(sqrt(x^2 + y^2))'); { index profile }
bp_set_R('R(z)', '');
bp_set_loss('loss(x, y)'); { simulate losses for cladding modes }
bp_set_A0('A_lm_xy(0, 1, lambda, x, y)'); { initial amplitude }
bp_set_interpol(2); { quadratic interpolation }
end
Ergebnisse
Anfangs nehmen wir an, dass die Biegung entlang der Faser immer stärker wird. Das ursprünglich in die Faser geschickte Licht ist in der fundamentalen Mode. Den inversen Krümmungsradius lassen wir linear mit der z-Position ansteigen. Abbildung 1 zeigt die Amplitudenverteilung in der y-z-Ebene.
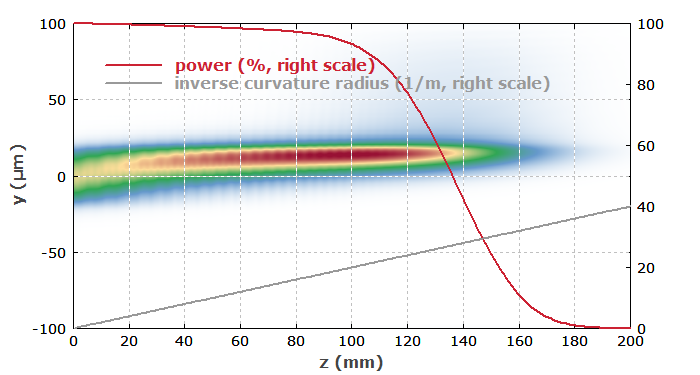
Man kann erkennen, dass das Intensitätsprofil der geführten Mode mehr und mehr von der Faserachse weggedrückt wird, und dass die optische Intensität wegen der Reduktion der Modenfläche zunimmt. Nach 100 mm ist die Modenfläche nur noch ca. halb so groß wie bei der gerade gehaltenen Faser. Von diesem Punkt an werden die Verluste recht stark: Das Licht wird mehr und mehr in die Cladding-Moden ausgekoppelt. Man sieht, dass die Biegeverluste kritisch werden, wenn der Biegeradius die Größenordnung von 50 mm erreicht.
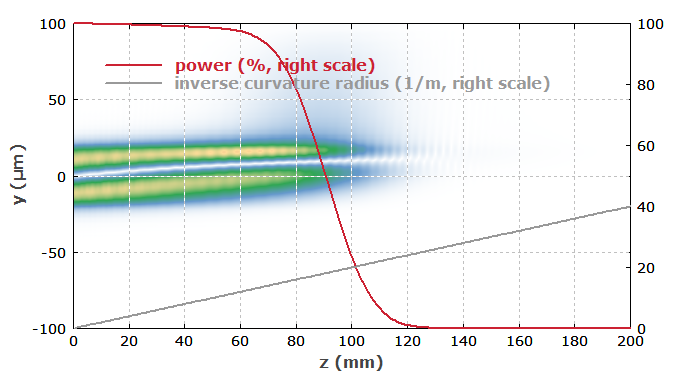
Wir können dasselbe für die LP11-Mode tun, siehe Abbildung 2. Hier setzen die Biegeverluste früher ein, und der Großteil der Leistung ist bereits nach 120 mm verloren.
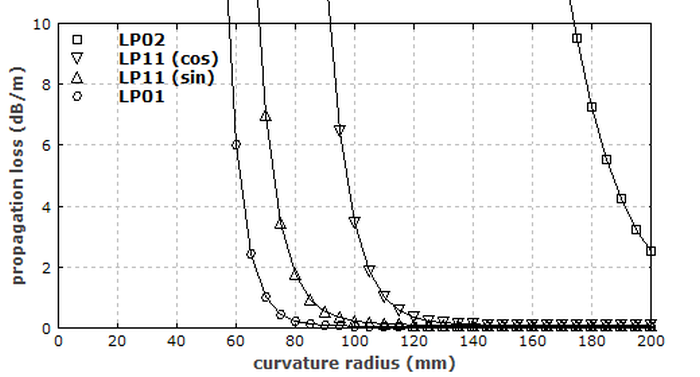
Es ist ebenfalls interessant, die Biegeverluste (in dB/m) für verschiedene Moden als Funktion des Krümmungsradius zu untersuchen. Anstatt separate Simulationsläufe für jeden Radius und jede Mode vorzunehmen, können wir eine einfache automatisierte Simulation vornehmen. Für jeden Satz von Werten lassen wir den Krümmungsradius kontinuierlich den jeweiligen Wert erreichen, lassen das Feld dann über eine gewisse Distanz propagieren, und dann über eine weitere Distanz für die Ermittlung der Biegeverluste. Dies braucht insgesamt etliche Minuten Rechenzeit, aber wir bekommen damit eine Menge von Daten: