RP Coating – Advanced Software for
Designing Optical Multilayer Structures

Here, we design a thin-film polarizer in the form of a polarizing cube, where the multilayer thin-film coating is embedded between two 45° prisms.

The basic idea of the common MacNeille cube design is to eliminate the reflection for p polarization by having Brewster's angle at all internal interfaces. It is then easy to obtain high reflectivity for s polarization with a simple Bragg mirror design without introducing a significant reflection for p polarization. The Brewster angle condition requires that a substrate material with suitable refractive index (for given coating materials) is chosen. For the outer interfaces, one requires anti-reflection coatings, which are not considered here.

We seek for a design working well between 900 nm and 1200 nm. First we need to choose the materials. If we decide for TiO₂ and SiO₂ layers in the coating, we need a substrate material with a suitable refractive index in order to meet the above-mentioned Brewster condition. We use an equation for calculating the optimum substrate index, and have found that Schott SF11 glass comes relatively close:

d_units: nm
l_units: nm
 
l := 1064  { operation wavelength }
 
n_L := n_SiO2(l * l_units)
n_H := n_TiO2(l * l_units)
n_S_opt := n_H * n_L / sqrt(n_H^2 + n_L^2) / sin(theta)
  { optimum substate index for a MaxNeille polarizer }
show "n_S_opt:   ", n_S_opt:f3
n_S(l) := n_SF11(l)  { chosen substrate material }
n_S := n_S(l * l_units)
show "n_S:       ", n_S:f3

We then implement the basic design:

theta_L := arcsin(n_S * sin(theta) / n_L)
d_L := (l / n_L / 4) / cos(theta_L)
theta_H := arcsin(n_S * sin(theta) / n_H)
d_H := (l / n_H / 4) / cos(theta_H)
N_Bragg := 4  { number of layer pairs }
 
beam from superstrate
substrate: S
for j := 1 to N_Bragg do
begin
* SiO2, d = d_L, d_max = 2 * d_L
* TiO2, d = d_H, d_max = 2 * d_H
end
* SiO2, d = d_L, d_max = 2 * d_L
superstrate: S

Then we define a figure-of-merit function describing the design goal:

FOM() := sum(l := 900 to 1200 step 5,
       sum(dtheta := -2 deg to +2 deg step 0.5 deg,
  R_p(l,theta + dtheta)^2 + 10 * T_s(l,theta + dtheta)^2))

Here, we consider some range of angles, and use a 10 times larger weight for the transmission for s polarization. (Such parameters can depend on the concrete requirements.)

We can then use a simple local optimization to further improve the performance:

optimize coating for minimum of FOM()

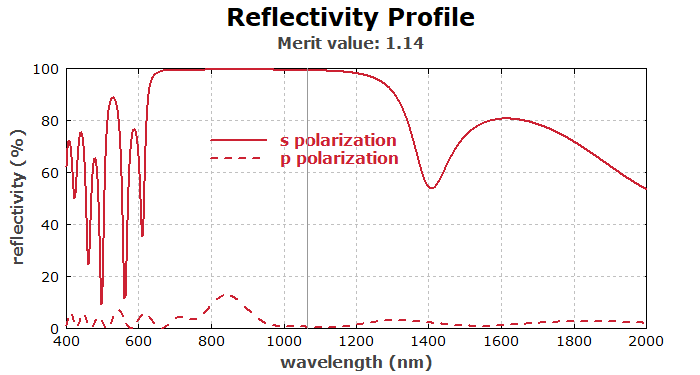
The first diagram made shows the reflectivity profile:

diagram 1:
 
"Reflectivity Profile"
 
["Merit value: ", FOM():d3]
 
x: 400, 2000
"wavelength (nm)", @x, size = %5
y: 0, 100
"reflectivity (%)", @y, size = %5
frame
hx
hy
legpos 420, 150
 
f: 100 * R_s(x, theta), "s polarization",
  color = red, width = 3, step = 1
 
f: 100 * R_p(x, theta), "p polarization", style = dashed,
  color = red, width = 3, step = 1
 
! begin
    setcolor(gray);
    line(l,l + i * CS_y2)
  end

We then test the sensitivity to angle changes:

diagram 2:
 
"Variation of the Angle of Incidence"
 
x: 40, 50
"angle of incidence (°)", @x
y: 0, 100
"reflectivity (%)", @y
frame
hx
hy
 
f: 100 * R_s(l, x * deg), "s polarization",
  color = red, width = 3
f: 100 * R_p(l, x * deg), "p polarization",
  color = red, width = 3, style = dashed

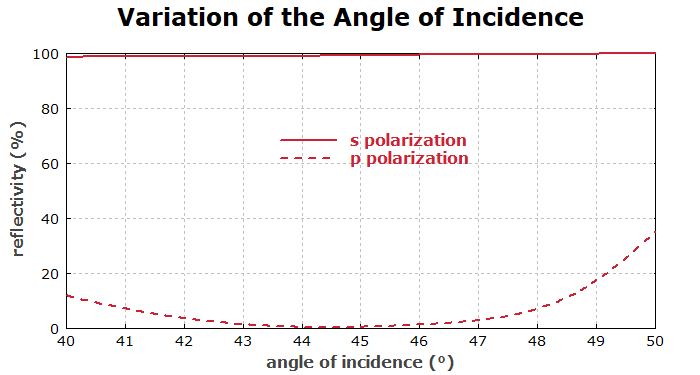
We see that a good performance is obtained only in a relatively narrow range of angles, which is typical for such designs.

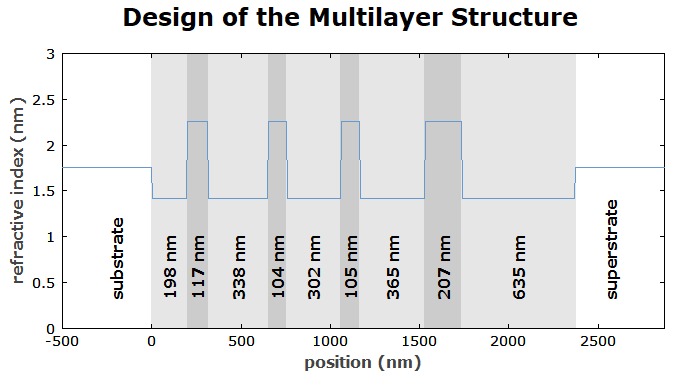
Finally, we show the design of the obtained structure:

diagram 3:
 
x: -500, get_d(0) + 500
"position (nm)", @x
y: 0, 3
"refractive index (nm)", @y
frame
 
! begin
    for j := 1 to nolayers() do
    begin
      var g;
      g := if get_material$(j) = "TiO2" then 0.8 else 0.9;
      setcolor(rgb(g, g, g));
      box(get_z(j), get_z(j + 1) + i * CS_y2);
    end;
    draw_cs(); { draw the coordinate system again }
  end
 
[get_d(j):f0:"nm"], (get_z(j) + 0.5 * get_d(j))l, (0.1 * CS_y2)c,
   direction = 90, for j := 1 to nolayers()
"substrate", (-200)l, (0.1 * CS_y2)c, direction = 90
"superstrate", (get_d(0) + 200)l, (0.1 * CS_y2)c, direction = 90
 
f: n(x,l), step = 1, color = blue