RP Coating – das Software-Werkzeug für das Design optischer Vielschichtstrukturen

Die hohe Flexibilität unserer Software ermöglicht auch kompliziertere Berechnungen. Als Beispiel betrachten wir hier einen Fall, in dem die optische Leistung in einer Struktur zu einer Aufheizung führt, die wiederum das optische Verhalten beeinflusst, so dass auch die Heizleistung davon verändert wird. Es muss mit einem iterativen Verfahren ein selbstkonsistenter Zustand des Systems gefunden werden.

Wir betrachten ein monolithisches Etalon, welches zwei Bragg-Spiegel auf den Seiten eines dielektrischen Spacers enthält, der gewisse Absorptionsverluste aufweist. Das Design wird wie folgt beschrieben:

d_units: nm
l_units: nm
 
l_Bragg := 1000  { Bragg wavelength }
N_Bragg := 4 { number of layer pairs }
d_sp := 0.1 mm / d_units { thickness of spacer }
n_sp := 1.5  { refractive index of spacer (for T = 0) }
n_i_sp := 1e-6  { imaginary component of refractive index of spacer }
dndT_sp := 3e-4 { temperature coefficient of spacer }
dTdP := 35  { thermal resistance in K/W }
 
beam from superstrate
substrate: air
for j := 1 to N_Bragg do
begin
  * SiO2, l/4 at l_Bragg
  * TiO2, l/4 at l_Bragg
end
* (n = n_sp + i * n_i_sp), d = d_sp
spacer := nolayers()
for j := 1 to N_Bragg do
begin
  * TiO2, l/4 at l_Bragg
  * SiO2, l/4 at l_Bragg
end
superstrate: air

Um die Effekte der Aufheizung des Spacers zu beschreiben, die durch die Absorption von Licht entsteht, definieren wir zunächst eine Funktion, mit der wir eine bestimmte Temperatur des Etalons setzen können:

set_T(T) := set_n(spacer, n_sp + dndT_sp * T + i * n_i_sp)

Dann definieren wir eine Funktion, die iterativ einen selbstkonsistenten Zustand des Systems berechnet:

T_h(l, P_inc, var dT) :=
  { Transmissivity for wavelength l and incident power P_inc,
    taking into account the heating of the spacer medium.
    The temperature increase is returned as dT;
    its initial value is also used. }
  begin
    global dTdP;
    const T_tol = 1e-4, dT_tol = 1e-3, max_N = 500;
    var T, N, T_l, dT_l, ok;
    set_T(dT);
    T := T(l); { calculate transmission for the given temperature }
    N := 0;
    repeat
      var P_dis;
      inc(N);
      T_l := T; { last transmission value }
      dT_l := dT; { last temperature change }
      P_dis := P_inc * (1 - T - R(l));
      dT := P_dis * dTdP;
      dT := 0.5 (dT + dT_l);
      set_T(dT);
      T := T(l); { recalculate for the new temperature }
      ok := abs(T - T_l) < T_tol and abs(dT - dT_l) < dT_tol;
    until ok or N = max_N;
    if ok then T else -1;
  end

Diese Version ist noch nicht perfekt bezüglich der Konvergenz; deswegen enthält ein Demo-Skript, das mit der Software geliefert wird, eine etwas ausgefeiltere Version, die eine variable Dämpfung der Temperaturentwicklung verwendet.

Nun können wir die optische Durchlässigkeit als Funktion der Wellenlänge für verschiedene einfallende optische Leistungen plotten, ebenfalls die Temperaturerhöhung für den Fall mit der höchsten Leistung:

diagram 1:
 
"Power-dependent Transmissivity Profile"
 
x: 998, 1002
"wavelength (nm)", @x
y: 0, 100
"transmissivity (%)", @y
frame
hx
hy
 
P_inc_max := 5
! dT := 0
f: 100 * T_h(x, P_inc, dT),
  width = 3,
  step = 1,
  maxconnect = 1,
  for P_inc := 0 to P_inc_max step 1,
  ["P_inc = ", P_inc:d3:"W"],
  color = color_I(0.1 + 0.9 * P_inc / P_inc_max)
 
! P_inc := P_inc_max
! dT := 0
f: (T_h(x, P_inc, dT); dT) * 10,
  color = magenta,
  width = 3,
  style = fdashed,
  step = 1,
  "temperature increase\\for max. power (a. u.)"

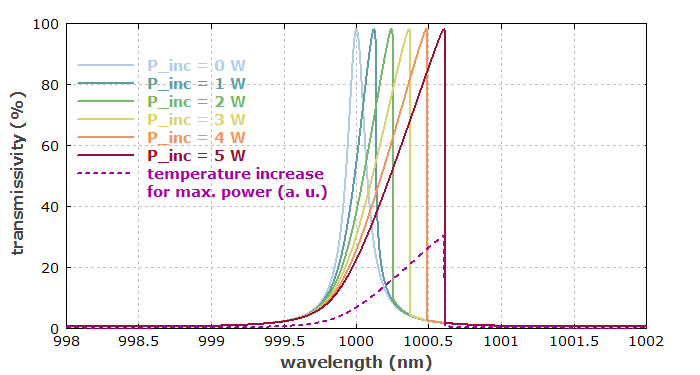
Man kann sehen, dass die Transmissions-Peaks des Etalons für höhere Leistungen immer asymmetrischer werden. Dies liegt daran, dass die resonant erhöhte optische Leistung eine verstärkte Aufheizung verursacht, die wiederum die Resonanzen in Richtung längerer Wellenlängen verschiebt. (Genau genommen entsteht der Effekt einerseits durch eine Erhöhung des Brechungsindex und andererseits durch die thermische Ausdehnung des Spacers; der Einfachheit halber können wir jedoch beide Effekte kombiniert über einen effektiv erhöhten Temperaturkoeffizienten des Brechungsindex beschreiben.)

Ein zweites Diagramm zeigt, was geschieht, wenn man die Resonanzen in beiden Richtungen scannt (für die höchste angewendete optische Leistung):

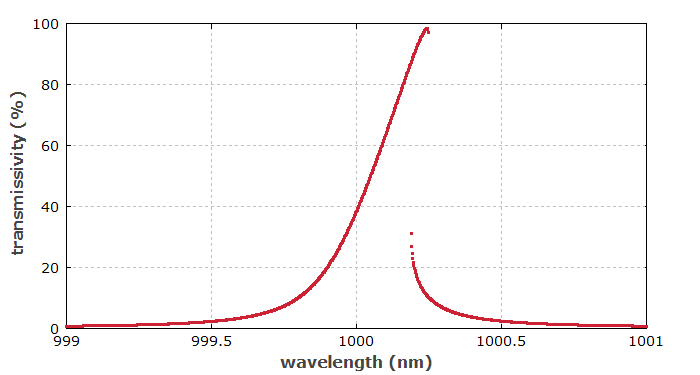
Wenn man bei kurzen Wellenlängen beginnt, kann man hohe Transmission bei ca. 1000.25 nm erhalten, wo die Resonanz nur noch durch die starke Aufheizung erreicht wird. Wenn man dagegen mit langen Wellenlängen beginnt, bleibt das System bei der genannten Wellenlänge in einem Zustand mit niedriger Transmission und geringerer Aufheizung. Ein solches bistabiles Verhalten wird bei solchen Systemen oft beobachtet. In unserem Beispielfall verschwindet es, wenn wir die Anzahl von Schichtpaaren in den Bragg-Spiegeln von 4 auf 3 reduzieren.