RP Coating – Advanced Software for
Designing Optical Multilayer Structures
| Overview | Purpose | Model | Interface | Demos | Versions |
Demo File: Dichroic Mirror
This is a simple demo file, not containing a custom form; the input are simply defined within the script. This case demonstrates how you can quickly get some calculations done with a few lines of script code.
Note that we also have a newer, more advanced version with a custom form.
We design a dichroic mirror with high reflectivity at 1064 nm and high transmission at 808 nm at normal incidence. Such mirrors are often used for pumping Nd:YAG and Nd:YVO4 lasers.
As an initial design, we use a simple Bragg mirror:
beam from superstrate substrate: BK7 for j := 1 to 8 do begin * TiO2, l / 4 at 1200 * SiO2, l / 4 at 1200 end superstrate: air
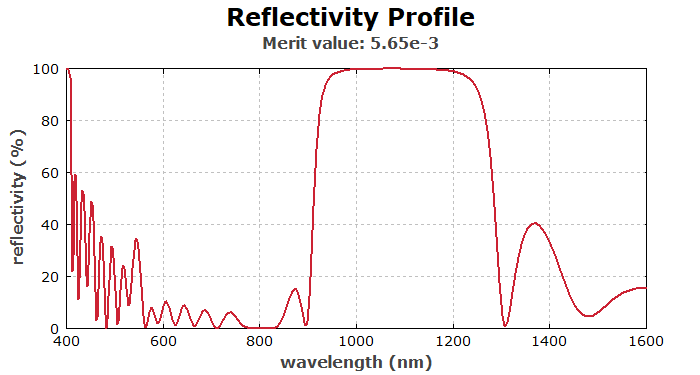
Such a mirror already has a high reflectivity at 1064 nm. The transmission at 808 nm, however, is not ideal, even though that wavelength is outside the main reflection band.
Then we define the figure-of-merit function describing the design goal:
d_units: nm
l_units: nm
l_HR := 1064 { HR wavelength }
l_HT := 808 { HT wavelength }
FOM() :=
sqrt(sum(d := -20 to +20 step 5, T(l_HR + d)^2)
+sum(d := -20 to +20 step 5, R(l_HT + d)^2))
With that, we “punish” any transmission around 1064 nm and any reflectivity around 532 nm. It is advantageous to demand such properties not only at isolated wavelengths, as that may lead to designs which are sensitive to fabrication errors.
We can then apply a simple local optimization:
optimize coating for minimum of FOM(), ytol = 1e-5
Next, we make a diagram showing the reflectivity profile:
diagram 1: "Reflectivity Profile" ["Merit value: ", FOM():d3] x: 400, 1600 "wavelength (nm)", @x y: 0, 100 "reflectivity (%)", @y frame hx hy f: 100 * R(x), color = red, width = 3
When executing the script, we get the following:
A second diagram is made for showing the obtained thin-film design:
diagram 2:
"Design of the Multilayer Structure"
x: -500, get_d(0) + 500
"position (nm)", @x
y: 0, 3
"refractive index (nm)", @y
frame
! begin
for j := 1 to nolayers() do
begin
var g;
g := if get_material$(j) = "TiO2" then 0.8 else 0.9;
setcolor(rgb(g, g, g));
box(get_z(j), get_z(j + 1) + i * CS_y2);
end;
draw_cs(); { draw the coordinate system again }
end
[get_d(j):f0:"nm"],
(get_z(j) + 0.5 * get_d(j))c, (0.1 * CS_y2)b, direction = 90,
for j := 1 to nolayers()
"substrate", (-200)c, (0.1 * CS_y2)b, direction = 90
"superstrate", (get_d(0) + 200)c, (0.1 * CS_y2)b, direction = 90
f: n(x, 1200), step = 1, color = blue
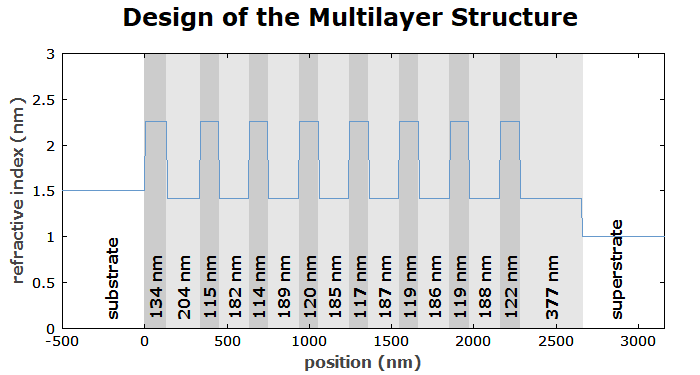
We see that this design does not deviate much from that of a simple Bragg mirror.
