Noise in Laser Technology – Part 3: Beam Pointing Fluctuations

When thinking about what causes beam pointing fluctuations of a laser, probably the first thought will be about mechanical vibrations. Indeed, vibrations of components of the laser resonator, in particular of mirrors, can directly affect the position and direction of the intracavity beam and thus also of the output beam.

However, one should not overlook another factor which can be more important, particularly in high-power lasers: thermal effects in a laser crystal can lead to a significant deflection of the intracavity laser beam, just as if a laser mirror had been somewhat misaligned. The strength of such effects depends not only on power levels and resonator designs, but also on the care with which the laser resonator is aligned. For imperfect alignment, the laser beam may not go exactly through the center of the thermal lens in the laser crystal. This will cause some deflection, which is dependent on the pump power, so that any pump power fluctuations will be translated into fluctuations of the beam position. Also, any asymmetric changes of the spatial pump beam profile can affect the beam position, even in cases with perfect alignment. It becomes apparent that a high stability of the beam position is easier to achieve when the pump beam profile is stable and highly symmetric. Therefore, the use of some effective beam homogenizer for the pump beam can be beneficial. A continuously operating pump source will also cause smaller problems than one which is turned on and off, as it is sometimes required.

Both vibrations and thermal effects can be considered as a dynamically changing misalignment. The involved frequencies are normally so low that the laser beam can be assumed to instantaneously find the position which fits to the momentary mirror positions – more precisely, it will have a position such that a nearly exactly closed beam path is obtained in any moment. This aspect greatly facilitates any theoretical treatment.

The sensitivity of a resonator to misalignments can be calculated – not with simple software based on the well-known ABCD matrix algorithm, which is often used for resonator design, but with advanced software [2] using an extended ABCDEF matrix algorithm [3]. Essentially, this algorithm allows one to calculate the effects of optical elements not only in terms of beam expansion and focusing, but also in terms of the local offset from the reference beam axis and the corresponding offset angle. The self-consistency condition for a full resonator round trip then determines the beam position for any combination of mirror misalignments.

As an example, we consider a simple laser resonator with a curved mirror M1, a laser crystal, and a plane output coupler mirror M2. The output beam is then collimated with a lens L1, and later on focused to a small spot with a second lens L2. Figure 1 shows how the beam radius evolves, and how the beam axis is shifted when the first mirror is tilted by ±0.5 mrad. As M2 is flat, the tilt of M1 can only cause a parallel shift of the beam axis. The collimation lens L1, however, translates that shift into an angular change. The focusing lens L2 again changes the beam offset and angle. At the focus, the beam offsets are more than half the beam radius, i.e., there is a significant shift of the focus caused by the mirror tilt.

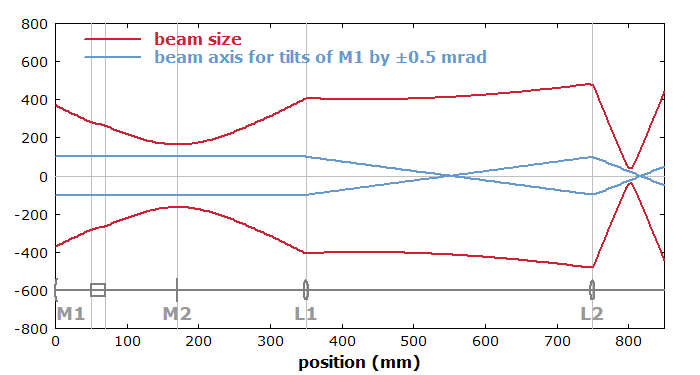
Figure 2 shows the situation for tilts of M2 instead of M1. Here, the laser's output beam obtains the same angular offset as M2. After the lens L2, however, the shift of the focus position is nearly zero. (This shift could even totally vanish if the distance between the lenses were increased to ∼534 mm.) On the other hand, the angular fluctuations at the focus will be larger in this case, but this might be irrelevant for the application.

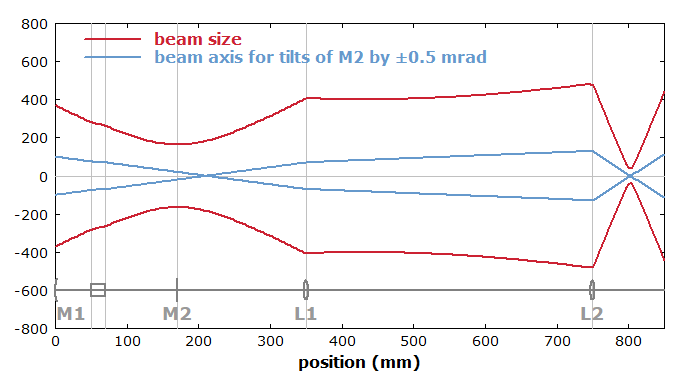
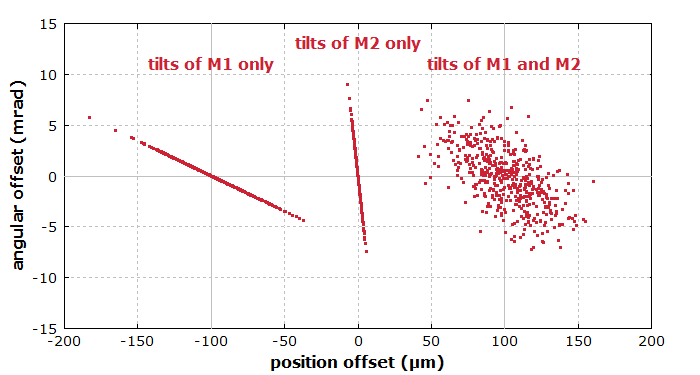
Figure 3 shows the effects of a random tilting of M1, M2 or of both mirrors simultaneously on the beam position and angular offset at the focus (at z = 802 mm). For tilts of a single mirror, changes of position and angle are fully correlated. This is no more the case when both mirrors are independently misaligned. We see again that tilts of M1 dominate the resulting fluctuations of focus position. We learn from the example case that the effects of mirror tilts can be rather different for different mirrors, and that the optics outside the laser resonator also have important effects.

In some cases, what counts is only the angular deviation of the laser's output beam from the reference axis. For example, this is the case when a collimated beam is directly sent to some distant target without further optics, or when it is tightly focused with a lens. However, in general the beam offset (lateral movement) at the laser output is also relevant. In the example case discussed above we could see that tilts of the left mirror have a substantially larger effect on the external beam focus, compared with tilts of the right mirror, even though the beam direction at the laser output is not affected. Obviously, the beam offset at the laser output is more important than the angular movement in that case.

One should also be aware that the output beam radius is important. Any beam offset at the laser output should be compared with the beam radius. Similarly, angular deviations should be compared with the natural beam divergence, which is smaller for beams with larger radius. For these reasons, it is quite meaningless to know the angular range of beam pointing fluctuations but not the output beam radius – as is often the case when reading data sheets.

A simple telescope can be used for increasing the beam radius at the laser output. It is easy to show that this will also increase fluctuations of the beam position while it will reduce the angular range of beam pointing fluctuations. This shows again that the larger the beam radius, the more severe will be some magnitude of angular fluctuations, and the less critical is the direct beam offset.

For optimizations, one should consider not only the laser, but the whole beam path to the application – for example, to a beam focus where materials are processed. With suitable software, one can identify the contributions of the tilts of all resonator mirrors and of thermal deflections on the beam position at that focus. It is also possible to calculate an overall figure of merit for the stability for a given design of laser resonator and external optics, and to numerically optimize the whole design for minimum beam pointing effects. Of course, this can involve trade-offs with other desirable properties, such as the beam quality, as discussed in the next paragraph.

For high-power lasers, beam pointing fluctuations are most difficult to minimize. There are essentially two reasons for that. The first one is that thermal effects tend to be strong in such lasers, and the often not very symmetric pump beam shapes make the problem even more severe. The second reason is that resonators with larger mode areas are generally more alignment-sensitive, and large mode areas are normally required for high-power lasers. This is particularly the case when a high beam quality is needed. Therefore, there is a trade-off between high beam quality and weak beam pointing fluctuations. Obviously, it is important to take into account such issues when designing robust high-power lasers for industrial use.

We have seen that beam pointing fluctuations can result from mirror vibrations and from thermal effects, and that both can be considered as a dynamical kind of resonator misalignment. The beam offset and angular fluctuations resulting from given fluctuations of mirror positions can be calculated with suitable software, which can also be used to optimize whole systems with respect to beam pointing effects. Clearly, minimizing such effects is not just a matter of a stable mechanical setup, but involves other aspects such as the resonator design and properties of the laser's pump beam. The external optics used between the laser and the application can also have an important influence.

Your question or comment:

Spam check:

  (Please enter the sum of thirteen and three in the form of digits!)

By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.

[1]	RP Photonics Encyclopedia: articles on laser noise, intensity noise, phase noise and others
[2]	Description of the software RP Resonator
[3]	O. E. Martínez, “Matrix formalism for dispersive laser cavities”, IEEE J. Quantum Electron. 25 (3), 296 (1989), doi:10.1109/3.18543
[4]	Part 1 – Intensity and Phase Noise
[5]	Part 2 – Fluctuations of Pulsed Lasers

(Suggest additional literature!)