Diffracted Angle and Littrow Angle of Reflective Gratings


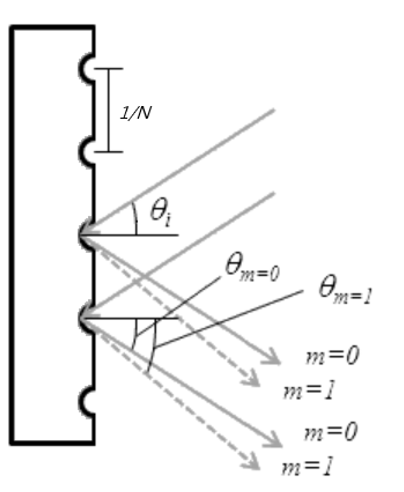
This Calculator Will Help You To calculate The Diffracted Angle For A Given Incidence Angle and The Littrow Angle of Reflective Gratings.

If m is negative, it means that the diffracted light and diffracted light are on the same side of the normal. If m is positive, it means that the diffracted light and diffracted light are on the opposite side of the normal.

$\frac{[ sin(\theta_m) + sin(\theta_i)]}{N}$= $m \lambda$

$\theta$=arcsin$\frac{N m \lambda}{2}$

Raster Line Density $N$; Incidence Angle $\theta_i$; Order $m$; Wavelength $\lambda$
Diffracted Angle $\theta_m$; Littrow Angle $\theta$;

Input
Raster Line Density, $N$:
1/mm
Incidence Angle, $\theta_i$:
degree (°)

Order, $m$:
Wavelength, $\lambda$:
nm


Output
Diffracted Angle, $\theta_m$:
degree (°)

Littrow Angle, $\theta$:
degree (°)